Các bài viết liên quan:
Permutation:
Bất kỳ sự sắp xếp nào của một tập hợp n đối tượng theo một thứ tự nhất định được gọi là Permutation của Đối tượng. Mọi sự sắp xếp bất kỳ r ≤ n của các đối tượng này theo một thứ tự nhất định được gọi là một Permutation r hoặc một Permutation của n đối tượng được lấy r tại một thời điểm.
Nó được ký hiệu là P (n, r)
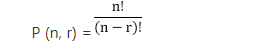
Định lý: Chứng minh rằng số Permutation của n vật được thực hiện tại một thời điểm là n !.
Bằng chứng: Chúng tôi biết rằng

Ví dụ:

Lời giải:

Permutation có hạn chế:
Số lần Permutation của n đối tượng khác nhau được thực hiện r tại một thời điểm mà p đối tượng cụ thể không xảy ra là

Số lần Permutation của n đối tượng khác nhau được thực hiện r tại một thời điểm mà p đối tượng cụ thể có mặt là

Ví dụ: Có thể lập bao nhiêu số có 6 chữ số bằng cách dùng các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8 nếu mọi số bắt đầu bằng ’30’ không có chữ số nào được lặp lại?
Lời giải: Tất cả các số bắt đầu bằng ’30. Do đó, chúng ta phải chọn 4 chữ số từ 7 chữ số còn lại.
∴ Tổng số các số bắt đầu bằng ’30’ là

Permutation với các đối tượng lặp lại:
Định lý: Chứng minh rằng số các Permutation khác nhau của n đối tượng phân biệt được thực hiện tại một thời điểm mà mọi đối tượng được phép lặp lại một số lần bất kỳ là nr.
Chứng minh: Giả sử rằng với n đối tượng, chúng ta phải điền vào r vị trí khi cho phép lặp lại đối tượng.
Do đó, số cách điền vào vị trí thứ nhất là = n
Số cách điền vào vị trí thứ hai = n
………………………..
………………………..
Số cách điền vào vị trí thứ r = n
Như vậy, tổng số cách điền r chỗ có n phần tử là
= n. N. n ………….. r lần = nr.
Permutation tròn:
Một Permutation được thực hiện xung quanh một vòng tròn được gọi là Permutation tròn.

Ví dụ: Có bao nhiêu cách xếp các chữ cái a, b, c, d, e, f, g, h, i, j thành một hình tròn?
Bài giải: (10 – 1) = 9! = 362880
Định lý: Chứng minh rằng số Permutation đường tròn của n vật thể khác nhau là (n-1)!
Chứng minh: Ta coi K là số Permutation cần thiết.
Với mỗi Permutation vòng như vậy của K thì có n Permutation tuyến tính tương ứng. Như đã trình bày trước đó, chúng ta bắt đầu từ mọi đối tượng của n đối tượng trong các Permutation vòng tròn. Như vậy, với K Permutation vòng, ta có K … n Permutation tuyến tính.

Combination
Combinations là sự lựa chọn một số hoặc tất cả các đối tượng từ một tập hợp các đối tượng nhất định, trong đó thứ tự của các đối tượng không quan trọng. Số lượng Combinations của n đối tượng, lấy r tại một thời điểm được biểu thị bằng nCr hoặc C (n, r).

Chứng minh: Số Permutation của n thứ khác nhau, lấy r tại một thời điểm được cho bởi
Vì không có vấn đề gì về thứ tự sắp xếp của các đối tượng, do đó, với mọi sự Combinations của r vật, đều có r! sắp xếp tức là,
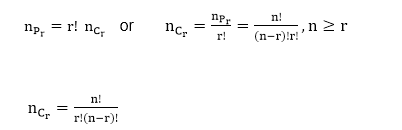
Ví dụ: Một người nông dân mua 3 con bò, 2 con lợn và 4 con gà mái từ một người đàn ông có 6 con bò, 5 con lợn và 8 con gà mái. Tìm số m cách chọn mà người nông dân có.
Người nông dân có thể chọn bò theo cách C (6, 3), lợn theo cách C (5, 2) và gà mái theo cách C (8, 4). Do đó số m cách chọn như sau:

Xem thêm Mã hóa ELGAMAL
Một số câu hỏi phổ biến về permutation và combinations
- Permutation và combinations là gì? Permutation và combinations là hai khái niệm trong toán học để đếm số cách sắp xếp hoặc chọn ra các phần tử từ một tập hợp cho trước.
- Permutation là gì? Permutation là số cách sắp xếp các phần tử của một tập hợp theo một trật tự nào đó. Số permutation của một tập hợp n phần tử là n! (n giai thừa).
- Combinations là gì? Combinations là số cách chọn ra k phần tử từ một tập hợp n phần tử mà không quan tâm đến thứ tự. Số combinations của một tập hợp n phần tử và k phần tử được tính bằng công thức C(n, k) = n!/[(n-k)!k!].
- Công thức chung để tính số permutation và combinations là gì?
- Số permutation của n phần tử được tính bằng n!.
- Số combinations của n phần tử và k phần tử được tính bằng C(n, k) = n!/[(n-k)!k!].
- Permutation và combinations khác nhau như thế nào?
- Permutation liên quan đến sự sắp xếp các phần tử trong một tập hợp, trong khi combinations liên quan đến sự lựa chọn các phần tử trong một tập hợp mà không quan tâm đến thứ tự.
- Số permutation của một tập hợp n phần tử là n!, trong khi số combinations của một tập hợp n phần tử và k phần tử được tính bằng công thức C(n, k) = n!/[(n-k)!k!].
- Trong Python, có thư viện nào hỗ trợ tính số permutation và combinations không? Trong Python, thư viện math hỗ trợ tính số permutation và combinations thông qua các hàm math.perm() và math.comb().
- Hàm math.perm() trong Python là gì? Hàm math.perm(n, k) trong Python trả về số permutation của n phần tử và k phần tử. Nó được tính bằng công thức n!/(n-k)!.
Ví dụ:
import math
n = 5
k = 2
# Tính số permutation của n phần tử và k phần tử
perm = math.perm(n, k)
print("Số permutation của", n, "phần tử và", k, "phần tử là:", perm)- Hàm math.comb() trong Python là gì? Hàm math.comb(n, k) trong Python trả về số combinations của n phần tử và k phần tử. Nó được tính bằng công thức n!/(n-k)!k!.
Ví dụ:
import math
n = 5
k = 2
# Tính số combinations của n phần tử và k phần tử
comb = math.comb(n, k)
print("Số combinations của", n, "phần tử và", k, "phần tử là:", comb)- Làm thế nào để tính số permutation hoặc combinations trong Python nếu không sử dụng thư viện math? Nếu không sử dụng thư viện math, ta có thể sử dụng hàm đệ quy để tính số permutation hoặc combinations. Ví dụ:
# Tính số permutation của n phần tử và k phần tử
def perm(n, k):
if k == 0:
return 1
else:
return n * perm(n - 1, k - 1)
# Tính số combinations của n phần tử và k phần tử
def comb(n, k):
if k == 0:
return 1
else:
return comb(n - 1, k - 1) * n // k
n = 5
k = 2
# Tính số permutation và combinations của n phần tử và k phần tử
perm = perm(n, k)
comb = comb(n, k)
print("Số permutation của", n, "phần tử và", k, "phần tử là:", perm)
print("Số combinations của", n, "phần tử và", k, "phần tử là:", comb)

