Số Pi, thường được biểu thị bằng ký hiệu (\pi), là một trong những hằng số toán học quan trọng nhất, nổi tiếng với vai trò của nó trong các công thức liên quan đến hình tròn và các hình học phức tạp khác. Giá trị của (\pi) xấp xỉ bằng 3.14159, nhưng nó là một số vô tỷ, có nghĩa là nó có một dãy số thập phân vô hạn không lặp lại. Trong toán học và khoa học, (\pi) được sử dụng để tính chu vi và diện tích của hình tròn, cũng như trong các công thức của vật lý liên quan đến hình học, như luật của Newton về chuyển động và trong lý thuyết tương đối của Einstein.
Trong lập trình, việc sử dụng (\pi) không kém phần quan trọng. Các ngôn ngữ lập trình như C++ cung cấp các hỗ trợ để làm việc với (\pi) thông qua thư viện toán học chuẩn. Trong C++, (\pi) có thể được truy cập thông qua hằng số M_PI sau khi bao gồm thư viện <cmath>. Sự hỗ trợ này cho phép các lập trình viên dễ dàng thực hiện các tính toán toán học và kỹ thuật chính xác, từ việc thiết kế đồ họa máy tính và mô phỏng vật lý đến việc phát triển các ứng dụng trong ngành kỹ thuật và khoa học vũ trụ.
Ví dụ, trong lập trình trò chơi hoặc thiết kế đồ họa, việc tính toán các đường cong, đường tròn, và các chuyển động xoay xung quanh một trục đều cần đến (\pi). Các chức năng như sin(), cos(), và tan(), được dùng để tính toán góc và chuyển động, cũng phụ thuộc nhiều vào (\pi). Sự hiểu biết về cách sử dụng (\pi) trong C++ mở ra vô số khả năng cho việc xây dựng các mô hình toán học phức tạp và chính xác, cung cấp công cụ mạnh mẽ cho các lập trình viên để họ tạo ra những giải pháp sáng tạo và hiệu quả.
Lịch sử của Số Pi
Số Pi, biểu tượng bằng ký tự Hy Lạp (\pi), là một trong những hằng số toán học cổ xưa và bí ẩn nhất, với lịch sử kéo dài hàng nghìn năm. Giá trị của (\pi) là tỷ số giữa chu vi của một hình tròn và đường kính của nó, và nó đã được khám phá và sử dụng trong nhiều nền văn minh cổ đại từ Ai Cập, Babylon, Ấn Độ cho đến Hy Lạp.
Nguồn Gốc và Lịch Sử Của Số Pi
- Babylon và Ai Cập cổ đại: Các tài liệu cổ từ Babylon (khoảng 1900 TCN) và Ai Cập (khoảng 1650 TCN) cho thấy những ước tính sơ bộ của (\pi), với giá trị lần lượt là 3.125 và 3.1605. Các nền văn minh này sử dụng (\pi) trong thiết kế kiến trúc và xây dựng.
- Archimedes của Syracuse: Archimedes (287–212 TCN) là một trong những nhà toán học đầu tiên cung cấp một phương pháp hệ thống để tính toán (\pi). Ông đã sử dụng phương pháp kiệt suất để ước lượng (\pi), bằng cách lồng ghép hình tròn trong các đa giác đều và tính toán chu vi của chúng.
Các Nhà Toán Học Đóng Góp vào Việc Nghiên Cứu và Tính Toán Số Pi
- Zu Chongzhi: Nhà toán học Trung Quốc này ở thế kỷ 5 đã tính (\pi) với độ chính xác đáng kinh ngạc lên đến bảy chữ số thập phân, một kỷ lục mà mãi đến thế kỷ 15 mới bị phá vỡ.
- Leonhard Euler: Vào thế kỷ 18, Euler đã sử dụng ký hiệu (\pi) mà chúng ta biết ngày nay và đưa nó trở thành chuẩn mực trong toán học. Euler cũng đã khám phá ra nhiều khía cạnh của (\pi), bao gồm cả các chuỗi vô hạn liên quan đến số này.
- Sự phát triển trong kỷ nguyên số hóa: Với sự ra đời của máy tính vào thế kỷ 20, (\pi) đã được tính toán với độ chính xác ngày càng cao. Những bước tiến trong công nghệ máy tính cho phép các nhà toán học và khoa học máy tính tính toán hàng tỷ chữ số của (\pi), với kỷ lục hiện nay là nhiều nghìn tỷ chữ số.
Khả năng thu hút sự quan tâm suốt nhiều thế kỷ và áp dụng rộng rãi trong nhiều lĩnh vực khoa học đã làm cho (\pi) trở thành một trong những số toán học được nghiên cứu nhiều nhất và phổ biến nhất. Sự tò mò về (\pi) không chỉ dừng lại ở các nhà toán học chuyên nghiệp mà còn lan rộng ra cả cộng đồng yêu thích toán học trên toàn thế giới.
Ý Nghĩa và Tính Chất của Số Pi
Số Pi ((\pi)) không chỉ là một trong những hằng số toán học được biết đến nhiều nhất mà còn là một trong những số có nhiều ứng dụng rộng rãi nhất trong toán học và khoa học. Giá trị của (\pi) khoảng 3.14159, nhưng nó là một số vô tỷ, có nghĩa là nó có một dãy số thập phân vô hạn không lặp lại và không thể biểu diễn chính xác dưới dạng tỷ lệ của hai số nguyên.
Ý Nghĩa Toán Học của Số Pi
(\pi) là tỷ số giữa chu vi của một hình tròn và đường kính của nó. Điều này có nghĩa là, cho bất kỳ hình tròn nào, chia chu vi của nó cho đường kính sẽ luôn cho kết quả là (\pi). Tính chất này làm cho (\pi) trở thành một khái niệm cơ bản trong hình học Euclid và hình học phân tích, nơi nó được sử dụng để tính toán chu vi và diện tích của các hình tròn cũng như thể tích và diện tích bề mặt của các hình cầu. Ngoài ra, (\pi) còn xuất hiện trong các công thức của hình học không gian, sóng và dao động, và là một phần không thể thiếu trong nghiên cứu về sóng điện từ và cơ học lượng tử.
Tính Chất Bất Thường của Pi
Số Vô Tỷ
(\pi) là một số vô tỷ, điều này có nghĩa là nó không thể được biểu diễn chính xác dưới dạng tỷ số của hai số nguyên. Khám phá này được chấp nhận rộng rãi sau công trình của nhà toán học Johann Lambert vào năm 1761, người đã chứng minh tính vô tỷ của (\pi) thông qua một chuỗi vô hạn.
Số Siêu Việt
Không chỉ là một số vô tỷ, (\pi) còn là một số siêu việt. Điều này có nghĩa là nó không phải là nghiệm của bất kỳ phương trình đa thức nào với hệ số hữu tỷ. Sự khám phá này được đưa ra bởi Ferdinand von Lindemann vào năm 1882, và nó đã đóng một vai trò quan trọng trong việc chứng minh rằng việc phân chia đường tròn thành một hình vuông bằng thước và compa là bất khả thi.
Sự phức tạp và tính bất thường của (\pi) không chỉ khiến nó trở thành một đối tượng nghiên cứu thú vị trong toán học mà còn chứng minh giá trị và tầm quan trọng của nó trong nhiều lĩnh vực khoa học. Việc hiểu sâu về (\pi) và các tính chất của nó giúp các nhà khoa học và kỹ sư giải quyết nhiều bài toán phức tạp liên quan đến hình học và vật lý.
Biểu Diễn Số Pi trong C++
Trong C++, số Pi ((\pi)) không có một định nghĩa chuẩn trực tiếp trong ngôn ngữ, nhưng nó có thể được biểu diễn và sử dụng một cách hiệu quả thông qua việc sử dụng thư viện <cmath>. Thư viện này cung cấp hằng số M_PI, đây là một trong những cách phổ biến nhất để làm việc với số Pi trong các chương trình C++ liên quan đến toán học và khoa học.
Biểu Diễn Số Pi trong C++
Trong thư viện <cmath>, M_PI được định nghĩa sẵn và biểu diễn giá trị xấp xỉ của (\pi), giúp người lập trình không cần phải tự định nghĩa số Pi khi cần sử dụng. Để sử dụng M_PI, người dùng cần đảm bảo rằng thư viện <cmath> đã được bao gồm trong chương trình.
Ví dụ về cách khai báo và sử dụng số Pi trong C++
Dưới đây là một ví dụ minh họa cách khai báo và sử dụng M_PI từ thư viện <cmath> để tính chu vi và diện tích của một hình tròn có bán kính nhất định.
#include <iostream>
#include <cmath> // Include to use M_PI
int main() {
double radius = 5.0; // Giả sử bán kính của hình tròn là 5 đơn vị
// Tính chu vi của hình tròn
double circumference = 2 * M_PI * radius;
std::cout << "Circumference of the circle: " << circumference << " units\n";
// Tính diện tích của hình tròn
double area = M_PI * radius * radius;
std::cout << "Area of the circle: " << area << " square units\n";
return 0;
}Trong ví dụ này, M_PI được sử dụng để thực hiện các phép tính liên quan đến chu vi và diện tích của hình tròn. Điều này không những giúp giảm thiểu lỗi khi nhập giá trị xấp xỉ của (\pi) mà còn đảm bảo tính chính xác và hiệu quả của chương trình.
Việc sử dụng M_PI trong C++ là một cách tiện lợi và chuẩn mực để làm việc với số Pi, giúp lập trình viên tránh được nhu cầu phải tự xác định và định nghĩa giá trị của (\pi), từ đó tập trung hơn vào logic và chức năng của chương trình.
Ứng Dụng của Số Pi trong Lập Trình
Số Pi ((\pi)) là một trong những hằng số toán học được sử dụng rộng rãi nhất trong lập trình, đặc biệt là trong các bài toán liên quan đến hình học và vật lý. Việc sử dụng số Pi không chỉ giới hạn ở các bài toán cơ bản như tính chu vi và diện tích hình tròn mà còn được áp dụng trong các bài toán nâng cao hơn, như phân tích hình dạng phức tạp và mô phỏng vật lý.
Minh họa Sử Dụng Số Pi Trong Các Bài Toán Thực Tế
Tính diện tích và chu vi hình tròn:
Đây là hai trong số các ứng dụng cơ bản nhất của số Pi. Công thức để tính chu vi (P) của hình tròn là (P = 2\pi r), và công thức để tính diện tích (A) là (A = \pi r^2), trong đó (r) là bán kính của hình tròn.
#include <iostream>
#include <cmath> // Include to use M_PI
int main() {
double radius = 10.0; // Bán kính của hình tròn
double circumference = 2 * M_PI * radius; // Tính chu vi
double area = M_PI * radius * radius; // Tính diện tích
std::cout << "Circumference: " << circumference << std::endl;
std::cout << "Area: " << area << std::endl;
return 0;
}Ứng Dụng Trong Các Bài Toán Nâng Cao
Tính toán các đặc tính của các hình dạng phức tạp:
Số Pi cũng đóng một vai trò quan trọng trong việc tính toán các đặc tính của các hình dạng phức tạp hơn, như hình elip, hình hyperbol, và trong các bài toán liên quan đến cơ học sóng và dao động.
Mô phỏng vật lý:
Trong mô phỏng vật lý, số Pi được sử dụng để mô phỏng các hiện tượng như chuyển động của các vật thể tròn, phân tích chuyển động trên quỹ đạo hình tròn hoặc elip (ví dụ, các hành tinh quay quanh mặt trời), và trong các phép tính liên quan đến động lực học chất lỏng và khí động lực học.
#include <iostream>
#include <cmath>
int main() {
double velocity = 30.0; // Vận tốc ban đầu của một vật thể được phóng đi với góc 45 độ
double angle = M_PI / 4; // Chuyển đổi góc thành radian
double gravity = 9.81; // Gia tốc trọng trường
// Tính toán khoảng cách mà vật thể di chuyển trước khi chạm đất
double range = (velocity * velocity * sin(2 * angle)) / gravity;
std::cout << "Range of the projectile: " << range << " meters" << std::endl;
return 0;
}Các ví dụ này chỉ là một số trong những cách thức mà số Pi được sử dụng trong lập trình để giải quyết các vấn đề thực tế, phản ánh sự đa dạng và tầm quan trọng của nó trong khoa học và kỹ thuật. Việc hiểu và sử dụng hiệu quả số Pi có thể mở rộng khả năng giải quyết vấn đề của lập trình viên và cung cấp những giải pháp sáng tạo cho các thách thức kỹ thuật.
Thuật Toán Tính Số Pi
Số Pi ((\pi)) là một trong những hằng số toán học được nghiên cứu nhiều nhất và có nhiều phương pháp khác nhau để tính toán giá trị của nó với độ chính xác cao. Trong số các phương pháp đó, chuỗi Leibniz và phương pháp Monte Carlo là hai thuật toán nổi bật, mỗi cái có những đặc điểm và ứng dụng riêng.
Chuỗi Leibniz
Chuỗi Leibniz cho (\pi) là một phương pháp sử dụng chuỗi vô hạn để tính toán (\pi). Nó được đặt theo tên của nhà toán học Đức, Gottfried Wilhelm Leibniz, mặc dù công thức này đã được nhà toán học Ấn Độ Madhava của Sangamagrama khám phá ra trước đó. Chuỗi Leibniz được biểu diễn như sau:
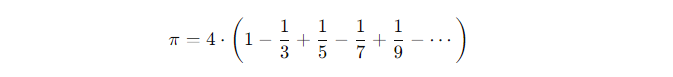
Phương Pháp Monte Carlo
Phương pháp Monte Carlo là một kỹ thuật sử dụng mô phỏng ngẫu nhiên để giải các bài toán toán học phức tạp, trong đó có việc ước tính (\pi). Ý tưởng chính là sử dụng một số lượng lớn điểm ngẫu nhiên để xác định tỷ lệ của các điểm rơi trong một hình tròn so với tổng số điểm trong một hình vuông bao quanh hình tròn đó.
Ví dụ Mã C++ cho Thuật Toán Tính Pi
Dưới đây là một ví dụ về cách sử dụng phương pháp Monte Carlo để ước tính (\pi) trong C++:
#include <iostream>
#include <cstdlib>
#include <ctime>
#include <cmath>
int main() {
srand(time(0)); // Khởi tạo bộ sinh số ngẫu nhiên
int trials = 1000000; // Số lượng điểm để mô phỏng
int circle_points = 0;
int square_points = 0;
for (int i = 0; i < trials; i++) {
double x = double(rand()) / RAND_MAX; // Sinh số ngẫu nhiên x trong khoảng [0,1]
double y = double(rand()) / RAND_MAX; // Sinh số ngẫu nhiên y trong khoảng [0,1]
double distance = x * x + y * y; // Tính khoảng cách từ điểm (x, y) đến gốc tọa độ
if (distance <= 1) circle_points++; // Kiểm tra nếu điểm nằm trong hình tròn
square_points++;
}
double pi = 4.0 * circle_points / square_points; // Tính toán giá trị ước tính của Pi
std::cout << "Estimated Pi = " << pi << std::endl;
return 0;
}Trong ví dụ này, chúng ta sử dụng một số lượng lớn điểm ngẫu nhiên để ước tính tỷ lệ giữa số điểm rơi vào trong một hình tròn đơn vị và tổng số điểm, từ đó tính được giá trị ước tính của (\pi). Phương pháp này rất hữu ích khi các phương pháp toán học truyền thống không khả thi hoặc quá phức tạp để triển khai.
Tài liệu Tham Khảo
Để đảm bảo tính chính xác và đáng tin cậy của thông tin trong bài viết này về “Số Pi trong C++”, chúng tôi đã tham khảo nhiều nguồn tài liệu uy tín. Dưới đây là danh sách các nguồn đã sử dụng:
- Sách “C++ Primer” bởi Stanley B. Lippman, Josée Lajoie, và Barbara E. Moo. Cuốn sách này cung cấp một cơ sở vững chắc về lập trình C++ và cũng đề cập đến cách sử dụng các hằng số như số Pi trong các ứng dụng lập trình.
- Trang web của cppreference.com. Đây là một nguồn tài nguyên quan trọng cho việc học và tham khảo về ngôn ngữ lập trình C++. Nó cung cấp các ví dụ minh họa và thông tin chi tiết về cách sử dụng hằng số số Pi trong C++.
- Bài viết “Calculating Pi with C++” trên trang web của GeeksforGeeks. Bài viết này cung cấp một số phương pháp để tính toán số Pi trong C++ và làm thế nào để sử dụng kết quả tính toán cho các ứng dụng lập trình.
- “The Joy of π” bởi David Blatner. Cuốn sách này không chỉ là một cuốn sách về toán học mà còn là một cuốn sách về lịch sử và văn hóa của số Pi, cung cấp cái nhìn toàn diện về tầm quan trọng và ứng dụng của số Pi trong cuộc sống hàng ngày.
- Bài viết “Pi (π)” trên trang web của Wolfram MathWorld. Bài viết này cung cấp một cái nhìn sâu rộng về các thuật toán tính toán số Pi, lịch sử của nó và ứng dụng của số Pi trong các lĩnh vực khác nhau của khoa học và kỹ thuật.
Chúng tôi khuyến khích bạn tham khảo các nguồn này để hiểu sâu hơn về số Pi và để nâng cao kiến thức của mình về chủ đề này trong lập trình C++ và ứng dụng khác.


