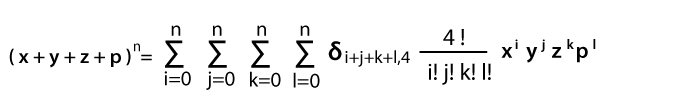Định lý đa thức được sử dụng để mở rộng lũy thừa của tổng của hai số hạng hoặc nhiều hơn hai số hạng. Định lý đa thức chủ yếu được sử dụng để tổng quát hóa định lý nhị thức thành đa thức với các số hạng có thể có một số bất kỳ. Tổng trọng số của các đơn thức có thể biểu diễn một lũy thừa (x1 + x2 + x3 +… .. + xk) n ở dạng x1b1, x2b2, x3b3… .. xkbk. Trong đó, các tổng quát của hệ số nhị thức, có thể được gọi là hệ số đa thức, được sử dụng để cung cấp trọng số. Chuỗi đa thức tương ứng có thể xuất hiện với sự trợ giúp của phân phối đa thức, có thể được mô tả như một tổng quát của phân phối nhị thức. Với sự trợ giúp của định lý này, chúng ta có thể mô tả kết quả của việc khai triển lũy thừa của đa thức.
Để mở rộng một biểu thức, định lý đa thức cung cấp một công thức, được mô tả như sau:
(x1 + x2 + ⋯ + xk) n với các giá trị nguyên của n
Chúng ta có thể mở rộng công thức này theo cách sau:

Với
n = n1 + n2 + n3 +…. + n và n! được sử dụng để mô tả ký hiệu giai thừa cho 1 * 2 * 3 *…. *N.
Hệ số
Trong đại số, trước tiên chúng ta phải học về cách chúng ta có thể đọc các phương trình đại số. Một số số hạng có trong cấu trúc đại số, được cộng hoặc trừ cùng nhau. Trong đại số, mỗi và mọi số hạng đều bao gồm hai phần là biến số và hệ số.
Trong thống kê, có một loại hệ số khác, được gọi là hệ số đa thức. Bây giờ chúng ta sẽ tìm hiểu về công dụng của hệ số đa thức trong thống kê.
Hệ số đa thức
Hệ số đa thức sử dụng chuỗi đa thức và sau đó lấy tên của nó. Chuỗi này được nâng lên sức mạnh thứ n, được mô tả như sau:

Trong chuỗi trên, x được sử dụng để mô tả các biến. K được sử dụng để mô tả số phần tử tồn tại trong chuỗi. Số n được sử dụng để mô tả lũy thừa số nguyên dương mà chuỗi được nâng lên. Định lý đa thức mô tả rằng cách loại chuỗi này được mở rộng, được mô tả như sau:

Tổng được lấy trên n1, n2, n3,…, nk trong định lý đa thức như n1 + n2 + n3 +… .. + nk = n.
Hệ số đa thức được sử dụng để cung cấp tổng của hệ số đa thức, hệ số này được nhân bằng cách sử dụng các biến. Nó được sử dụng để đại diện cho chuỗi mở rộng và mỗi số hạng trong chuỗi này chứa hệ số đa thức liên quan của nó. Về mặt thừa số, hệ số đa thức sẽ được biểu thị chính nó, được mô tả như sau:

Ví dụ về định lý đa thức
Ví dụ 1:
Trong ví dụ này, chúng ta sẽ khai triển (x + y + z) 3 như cách sau

Ví dụ 2:
Trong ví dụ này, chúng ta sẽ mô tả cách thức hoạt động của định lý đa thức đối với một tam thức. Đối với điều này, chúng tôi sẽ giả sử (x + y + z) 4. Nếu chúng ta sử dụng brute force để mở rộng biểu thức này, thì nó sẽ được viết như sau:
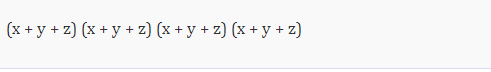
Bây giờ chúng ta sẽ áp dụng luật phân phối. Sau đó, chúng tôi sẽ đơn giản hóa bằng cách thu thập các điều khoản like. Biểu thức này có 81 điều khoản trước khi thu thập và sau khi phân phối. Lý do đằng sau 81 số hạng là mọi số hạng trong ngoặc thứ nhất sẽ được nhân với mọi số hạng trong ngoặc thứ hai, điều này sẽ cung cấp cho chúng ta 9 số hạng. Bây giờ mỗi thuật ngữ nhất định có nghĩa là 9 số hạng sẽ được nhân với mọi số hạng trong dấu ngoặc thứ ba, điều này sẽ cung cấp cho chúng ta 27 điều khoản. Cuối cùng, mỗi thuật ngữ cho trước có nghĩa là 27 số hạng sẽ được nhân với mỗi số hạng trong dấu ngoặc thứ tư, điều này sẽ cung cấp cho chúng ta 81 điều khoản. Trước khi đơn giản hóa, rất nhiều thuật ngữ sẽ trông khác nhau, nhưng khi chúng ta đơn giản hóa nó, thì nó sẽ trông giống hệt nhau.
Ví dụ: Giả sử chúng ta có bốn số hạng xyyy, yxyy, yyxy và yyyx. Theo các thuật ngữ này, x đến từ dấu ngoặc thứ nhất, thứ hai, thứ ba hoặc thứ tư. Khi chúng tôi đơn giản hóa các điều khoản này, thì chúng sẽ được thu thập và cung cấp dưới dạng 4xy3.

Trong khai triển trên, chúng ta có thể thấy rằng chúng ta có tổng cộng 15 số hạng riêng biệt, và mỗi số hạng chứa bậc 4. Hệ số cộng lên là 34 = 81.
Bây giờ chúng ta sẽ sử dụng các bước để xây dựng khai triển này và suy ra định lý đa thức như sau:
Bước 1: Chúng tôi sẽ sử dụng ba tổng kết lồng nhau để bắt đầu việc này:
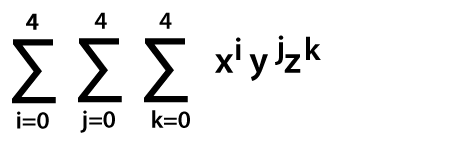
Vấn đề chúng ta gặp phải khi thực hiện việc này là phép tổng ba tạo ra 5 * 5 * 5 = 125 số hạng ở các mức độ khác nhau, mô tả phạm vi từ x0y0z0 đến x4y4z4.
Bước 2: Bây giờ, chúng tôi sẽ thêm hệ số lọc, hệ số này bằng 0 cho các cụm từ không mong muốn và 1 cho các cụm từ mong muốn. Đây được gọi là hàm delta Kronecker, và nó được ký hiệu là δi, j. Cú pháp để xác định điều này như sau:

Bây giờ chúng tôi sẽ thay đổi điều này như thế này:
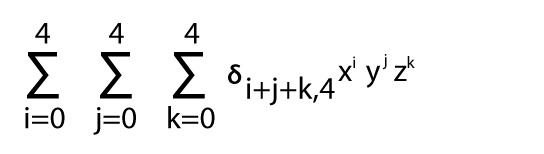
Tổng trên chỉ chứa 15 số hạng mong muốn, có bậc 4. Bây giờ chúng ta có một bài toán duy nhất là mọi hệ số đều bằng 1.
Bước 3: Bây giờ, chúng ta sẽ xây dựng hệ số chính xác. Hệ số này sẽ được gọi là hệ số đa thức như sau:

Số cách xếp 4 đối tượng phân biệt thành 3 nhóm riêng biệt sẽ được cung cấp bởi hệ số đa thức trên. Đối tượng tôi sẽ được gửi vào nhóm đầu tiên. Đối tượng j sẽ được gửi vào nhóm thứ hai và đối tượng k sẽ được ký gửi vào nhóm thứ ba. Không quan trọng là chúng tôi gửi chúng theo thứ tự nào.
Ví dụ: Trong hệ số của số hạng x1y1z2 sử dụng i = 1, j = 1 và k = 2, sẽ bằng

Với hệ số trên, khai triển sẽ được đọc như sau:
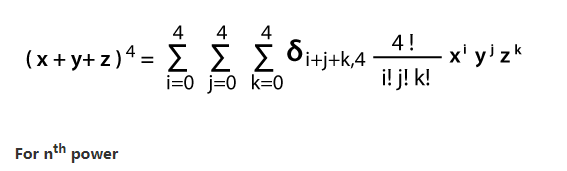
Bốn số hạng trên có thể được tổng quát thành lũy thừa thứ n của một tam thức. Đối với điều này, chúng ta phải thay đổi tất cả 4’s thành n’s.
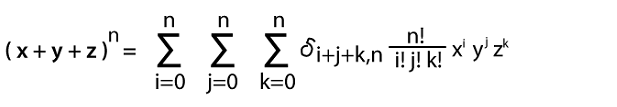
Đây được gọi là định lý đa thức cho 3 số hạng. Chúng ta có thể dễ dàng tổng quát số hạng thứ n thành bất kỳ số hạng nào. Ví dụ: đối với 4 số hạng, định lý đa thức sẽ được đọc như sau: