Giả sử một nhân viên bán hàng muốn đến thăm một số thành phố nhất định được giao cho anh ta. Anh ta biết khoảng cách của cuộc hành trình giữa mọi cặp thành phố. Vấn đề của anh ta là chọn một con đường bắt đầu từ thành phố quê hương của anh ta, đi qua mỗi thành phố chính xác một lần và trở về thành phố quê hương của anh ta một khoảng cách ngắn nhất có thể. Bài toán này liên quan mật thiết đến việc tìm một đoạn mạch Hamilton có độ dài nhỏ nhất. Nếu chúng ta biểu diễn các thành phố bằng các đỉnh và đường nối hai cạnh của các thành phố, chúng ta sẽ có được một đồ thị có trọng số trong đó, với mỗi cạnh ei một số wi (trọng số) được liên kết.
Các bài viết liên quan:
Một cách giải thích vật lý của phần tóm tắt trên là: coi đồ thị G như một bản đồ gồm n thành phố trong đó w (i, j) là khoảng cách giữa các thành phố i và j. Một nhân viên bán hàng muốn có chuyến tham quan các thành phố bắt đầu và kết thúc tại cùng một thành phố bao gồm việc đến thăm từng thành phố còn lại một lần và chỉ một lần.
Trong đồ thị, nếu chúng ta có n đỉnh (thành phố), thì có (n-1)! Các cạnh (tuyến đường) và tổng số mạch Hamilton trong một complete graph gồm n đỉnh sẽ là Bài toán Người bán hàng làm du lịch.
Cách giải Travelling Salesman Problem
Traveling Salesman Problem (TSP) là một trong những bài toán nổi tiếng trong lĩnh vực tối ưu hóa kinh tế và máy tính. Bài toán yêu cầu tìm một đường đi qua mỗi điểm trong một tập hợp các địa điểm du lịch (hay các thành phố) một lần duy nhất và kết thúc tại điểm xuất phát sao cho tổng chi phí của đường đi là nhỏ nhất.
Hiện nay vẫn chưa có phương pháp nào để giải quyết bài toán TSP một cách hoàn toàn tối ưu trong thời gian chấp nhận được. Tuy nhiên, các thuật toán heuristics và metaheuristics có thể được sử dụng để tìm giải pháp gần đúng.
Các phương pháp giải quyết bài toán TSP bao gồm:
- Brute Force: Tính toán tất cả các hoán vị của các điểm và chọn hoán vị tối ưu. Tuy nhiên, phương pháp này không thực tế cho các bài toán lớn vì số lượng hoán vị là rất lớn.
- Nearest Neighbor: Bắt đầu từ một điểm bất kỳ, tìm điểm gần nhất và di chuyển đến nó, sau đó tìm điểm gần nhất với điểm đang đứng và tiếp tục cho đến khi tất cả các điểm được ghé thăm. Phương pháp này dễ triển khai và thường được sử dụng cho các bài toán nhỏ.
- Christofides Algorithm: Kết hợp giữa Nearest Neighbor và Minimum Spanning Tree để tìm một lời giải gần đúng với tỷ lệ gần 3/2 so với giải tối ưu. Phương pháp này được sử dụng cho các bài toán lớn.
- Simulated Annealing: Một phương pháp metaheuristics, nó tạo ra một lời giải bắt đầu ngẫu nhiên và sau đó cố gắng tìm một lời giải tốt hơn bằng cách di chuyển qua các lời giải khác theo một quy trình tương tự như quá trình làm mát trong hàn.
- Genetic Algorithm: Một thuật toán tối ưu hóa được lấy cảm hứng từ các quá trình tiến hóa trong tự nhiên. Thuật toán này sử dụng một quần thể các lời giải và tiến hành các phép lai ghép, đột biến để tìm ra lời giải tốt hơn.
Phương pháp Nearest Neighbour
Thủ tục này mang lại kết quả hợp lý tốt cho vấn đề nhân viên bán hàng đi du lịch. Phương pháp như sau:
Bước 1: Chọn một đỉnh tùy ý và tìm đỉnh gần với đỉnh bắt đầu nhất để tạo thành đường đi ban đầu của một cạnh.
Bước 2: Gọi v là đỉnh mới nhất được thêm vào đường dẫn. Bây giờ, trong số kết quả của các đỉnh không nằm trong đường dẫn, hãy chọn đỉnh gần nhất với v và thêm đường dẫn, đường nối cạnh v và đỉnh này. Lặp lại bước này cho đến khi tất cả các đỉnh của đồ thị G được đưa vào đường dẫn.
Bước 3: Nối đỉnh bắt đầu và đỉnh cuối cùng bằng một cạnh và tạo thành mạch.
Ví dụ: Sử dụng phương pháp hàng xóm gần nhất để giải bài toán TSP sau đây, cho đồ thị được hiển thị trong hình bắt đầu từ đỉnh v1.
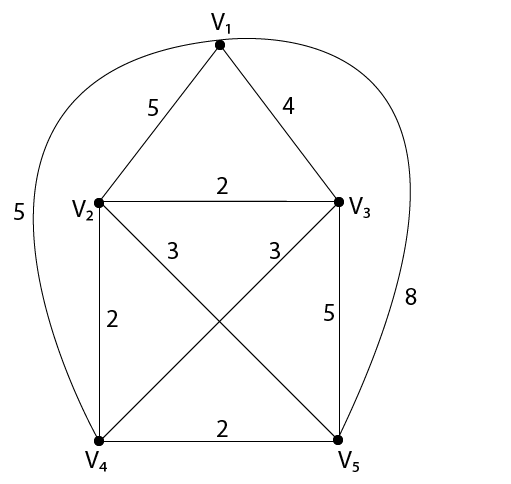
Giải pháp: Chúng ta phải bắt đầu với đỉnh v1. Bằng cách sử dụng phương pháp lân cận gần nhất, việc xây dựng đỉnh bằng đỉnh của chuyến tham quan hoặc mạch Hamilton được thể hiện trong hình:
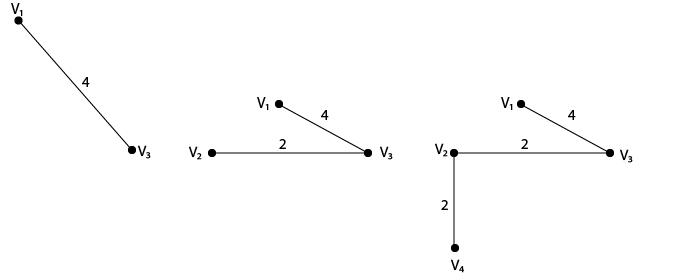
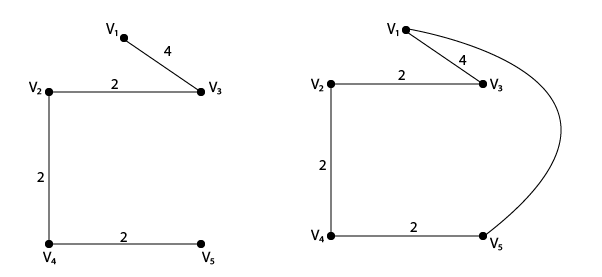
Tổng khoảng cách của tuyến đường này là 18.


