Python, một ngôn ngữ lập trình đa năng với cú pháp rõ ràng và mạnh mẽ, đã trở thành một công cụ không thể thiếu trong lĩnh vực khoa học dữ liệu. Sự linh hoạt và khả năng mở rộng của nó, cùng với một hệ sinh thái phong phú các thư viện dành cho việc phân tích dữ liệu, trực quan hóa, và máy học, đã khiến Python trở thành lựa chọn hàng đầu cho các nhà khoa học dữ liệu, nhà phân tích, và các chuyên gia AI trên toàn cầu.
Trong quá trình đưa ra quyết định dựa trên dữ liệu, phân tích thống kê đóng một vai trò quan trọng. Nó không chỉ giúp chúng ta hiểu được xu hướng, mối quan hệ, và mẫu trong dữ liệu mà còn cung cấp cơ sở cho việc kiểm định các giả thuyết và dự đoán. Từ việc tính toán các chỉ số thống kê mô tả cơ bản như trung bình, trung vị, và độ lệch chuẩn, đến việc thực hiện phân tích suy luận và mô hình hóa dự đoán, phân tích thống kê là nền tảng không thể thiếu trong việc khai thác giá trị từ dữ liệu.
Mục tiêu của bài viết này là cung cấp một cái nhìn tổng quan về cách thức sử dụng Python để thực hiện các phân tích thống kê. Bắt đầu từ việc giới thiệu các thư viện thống kê cơ bản như numpy và scipy, cho đến các thao tác phân tích dữ liệu phức tạp hơn với pandas và statsmodels, bài viết sẽ hướng dẫn bạn qua một loạt các kỹ thuật và phương pháp thống kê, từ cơ bản đến nâng cao. Dù bạn là người mới bắt đầu hay đã có kinh nghiệm, bài viết sẽ cung cấp cho bạn kiến thức và công cụ cần thiết để tận dụng sức mạnh của Python trong việc phân tích thống kê, giúp bạn đưa ra những quyết định dựa trên dữ liệu chính xác và hiệu quả.
Cài đặt và Thiết lập Môi trường
Để bắt đầu làm việc với phân tích thống kê sử dụng Python, điều đầu tiên cần làm là cài đặt Python và thiết lập môi trường làm việc. Python có thể được cài đặt trực tiếp từ trang web chính thức, nhưng một cách tiện lợi và phổ biến hơn là sử dụng bản phân phối Anaconda. Anaconda là một bản phân phối Python miễn phí và dễ sử dụng cho khoa học dữ liệu và máy học, cung cấp một môi trường ổn định cho cả Python và R, bao gồm hơn 1500 thư viện khoa học dữ liệu phổ biến.
Cài Đặt Python Thông Qua Anaconda
- Tải Anaconda: Truy cập trang web Anaconda và tải bản cài đặt phù hợp với hệ điều hành của bạn (Windows, MacOS, Linux).
- Cài Đặt Anaconda: Mở tệp đã tải và làm theo hướng dẫn để cài đặt. Trong quá trình cài đặt, bạn có thể chọn “Add Anaconda to my PATH environment variable”, tuy nhiên, điều này không được khuyến khích vì có thể gây xung đột với các bản Python khác. Thay vào đó, sử dụng Anaconda Prompt để truy cập môi trường Anaconda.
- Kiểm Tra Việc Cài Đặt: Mở Anaconda Prompt và gõ
python --versionđể kiểm tra phiên bản Python đã cài đặt.
Thiết Lập Môi Trường Làm Việc
Anaconda Navigator là một giao diện đồ họa giúp quản lý các môi trường và gói một cách dễ dàng. Bạn cũng có thể sử dụng Anaconda Prompt để tạo và quản lý môi trường làm việc.
- Tạo Môi Trường Mới: Sử dụng lệnh
conda create --name myenv python=3.8trong Anaconda Prompt, thaymyenvbằng tên môi trường của bạn và3.8bằng phiên bản Python mong muốn. - Kích Hoạt Môi Trường: Sau khi tạo, sử dụng lệnh
conda activate myenvđể kích hoạt môi trường. - Cài Đặt Thư Viện: Cài đặt các thư viện cần thiết bằng cách sử dụng lệnh
conda install numpy scipy pandas matplotlib seaborntrong môi trường đã kích hoạt.
Sử Dụng Jupyter Notebook
Jupyter Notebook là một ứng dụng web cho phép bạn tạo và chia sẻ các tài liệu có chứa mã số, công thức, hình ảnh và văn bản phong phú. Đây là công cụ lý tưởng cho việc thử nghiệm và trình bày phân tích dữ liệu.
- Cài Đặt: Trong môi trường đã kích hoạt, cài đặt Jupyter Notebook bằng lệnh
conda install jupyter. - Chạy Jupyter Notebook: Gõ
jupyter notebooktrong Anaconda Prompt hoặc terminal để khởi chạy. Một cửa sổ trình duyệt sẽ tự động mở, hiển thị giao diện người dùng của Jupyter Notebook, nơi bạn có thể tạo và quản lý các notebook.
Các thư viện thống kê
Trong lĩnh vực khoa học dữ liệu và phân tích thống kê, Python cung cấp một loạt các thư viện mạnh mẽ và linh hoạt. Ba thư viện chính được sử dụng rộng rãi bao gồm numpy, scipy, và pandas, mỗi thư viện có những ưu điểm và ứng dụng riêng biệt.
Numpy
Numpy (Numerical Python) là thư viện cốt lõi cho tính toán khoa học trong Python. Nó cung cấp hỗ trợ cho các mảng nhiều chiều lớn và các ma trận, cùng với một bộ lớn các hàm toán học để thực hiện các phép tính trên mảng này một cách hiệu quả. Numpy thích hợp cho việc thực hiện các phép tính toán học và thống kê cơ bản, như phép cộng, nhân ma trận, tìm kiếm min/max, trung bình, trung vị,…
Scipy
Scipy (Scientific Python) xây dựng trên Numpy, cung cấp một bộ công cụ toán học mở rộng, bao gồm các hàm cho tối ưu hóa, đại số tuyến tính, tích phân, nội suy, đặc biệt là các hàm thống kê. Thư viện này phù hợp cho các ứng dụng thống kê và kỹ thuật sâu hơn, bao gồm kiểm định giả thuyết, phân tích phương sai, và nhiều kỹ thuật thống kê suy luận khác.
Pandas
Pandas là một thư viện có sức mạnh và dễ sử dụng cho phân tích dữ liệu và làm việc với dữ liệu dạng bảng trong Python. Nó cung cấp các đối tượng DataFrame và Series, cho phép thực hiện các thao tác dữ liệu phức tạp một cách dễ dàng, như tổng hợp, tái cấu trúc, và lọc dữ liệu. Pandas đặc biệt hữu ích trong việc xử lý và phân tích dữ liệu thực tế, như dữ liệu tài chính, thời gian, và dữ liệu phức tạp khác cần phải được làm sạch và biến đổi trước khi phân tích.
So Sánh và Lựa Chọn Thư Viện Phù Hợp
- Numpy là lựa chọn tốt nhất cho việc thực hiện các phép toán ma trận và vector cơ bản, nơi hiệu suất tính toán là ưu tiên hàng đầu.
- Scipy mở rộng khả năng của Numpy bằng cách thêm vào các hàm thống kê và toán học phức tạp, làm cho nó trở thành lựa chọn tốt cho các bài toán cần đến thống kê suy luận và các phân tích toán học nâng cao.
- Pandas là thư viện tốt nhất cho việc xử lý và phân tích dữ liệu dạng bảng, nhờ khả năng làm việc với dữ liệu thực tế và cung cấp các công cụ mạnh mẽ để làm sạch, tổng hợp và biến đổi dữ liệu.
Lựa chọn thư viện phù hợp phụ thuộc vào nhu cầu cụ thể của dự án và loại dữ liệu bạn đang làm việc.
Phân tích thống kê mô tả
Phân tích thống kê mô tả là quá trình mô tả và tổng hợp dữ liệu thông qua các chỉ số thống kê, giúp chúng ta hiểu rõ các đặc tính chính của dữ liệu. Các khái niệm cơ bản trong phân tích thống kê mô tả bao gồm trung bình (mean), trung vị (median), mode (mốt), phạm vi (range), phương sai (variance), và độ lệch chuẩn (standard deviation).
- Trung bình (Mean): Là tổng của tất cả giá trị trong tập dữ liệu chia cho số lượng giá trị.
- Trung vị (Median): Là giá trị ở giữa của tập dữ liệu đã được sắp xếp.
- Mode (Mốt): Là giá trị xuất hiện thường xuyên nhất trong tập dữ liệu.
- Phạm vi (Range): Là sự chênh lệch giữa giá trị lớn nhất và nhỏ nhất trong tập dữ liệu.
- Phương sai (Variance): Đo lường mức độ phân tán của dữ liệu so với trung bình.
- Độ lệch chuẩn (Standard Deviation): Căn bậc hai của phương sai, cũng đo lường sự phân tán của dữ liệu.
Sử Dụng Pandas và Numpy để Tính Toán Các Chỉ Số Thống Kê Mô Tả
Sử dụng Pandas:
import pandas as pd
# Tạo DataFrame
data = {'Scores': [23, 45, 56, 78, 33]}
df = pd.DataFrame(data)
# Tính toán
mean = df['Scores'].mean()
median = df['Scores'].median()
mode = df['Scores'].mode()[0]
range_value = df['Scores'].max() - df['Scores'].min()
variance = df['Scores'].var()
std_dev = df['Scores'].std()
print(f'Mean: {mean}\nMedian: {median}\nMode: {mode}\nRange: {range_value}\nVariance: {variance}\nStandard Deviation: {std_dev}')Sử dụng Numpy:
import numpy as np
# Tạo mảng dữ liệu
scores = np.array([23, 45, 56, 78, 33])
# Tính toán
mean = np.mean(scores)
median = np.median(scores)
# Numpy không có hàm mode, sử dụng scipy hoặc pandas cho mode
range_value = np.ptp(scores)
variance = np.var(scores)
std_dev = np.std(scores)
print(f'Mean: {mean}\nMedian: {median}\nRange: {range_value}\nVariance: {variance}\nStandard Deviation: {std_dev}')Trong ví dụ trên, chúng ta đã tạo một tập dữ liệu đơn giản bao gồm các điểm số, sau đó sử dụng Pandas và Numpy để tính toán các chỉ số thống kê mô tả chính. Mỗi thư viện cung cấp những phương tiện tiện lợi và mạnh mẽ để thực hiện phân tích thống kê mô tả, giúp chúng ta hiểu rõ hơn về cấu trúc và đặc điểm của dữ liệu mà chúng ta đang làm việc.
Phân tích thống kê suy luận
Phân tích thống kê suy luận là một nhánh quan trọng của thống kê, cho phép chúng ta rút ra kết luận về một quần thể dựa trên một mẫu dữ liệu. Hai khái niệm cơ bản trong phân tích thống kê suy luận là ước lượng (đánh giá các thông số quần thể như trung bình hoặc tỉ lệ) và kiểm định giả thuyết (kiểm tra các giả định về quần thể). Phân tích thống kê suy luận thường sử dụng các phương pháp như kiểm định t (t-test), phân tích phương sai (ANOVA), và kiểm định chi-square (chi-squared test).
Kiểm Định t (T-Test) Sử Dụng Scipy
Kiểm định t được sử dụng để xác định xem có sự khác biệt đáng kể giữa các trung bình của hai nhóm dữ liệu. Dưới đây là ví dụ sử dụng scipy:
from scipy import stats
# Dữ liệu: điểm số của hai lớp học
class1_scores = [88, 92, 94, 95, 96]
class2_scores = [91, 92, 93, 94, 95]
# Thực hiện kiểm định t
t_stat, p_value = stats.ttest_ind(class1_scores, class2_scores)
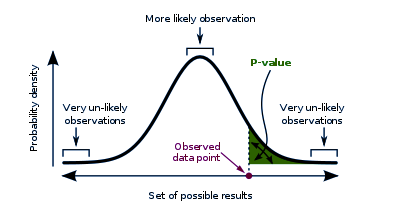
print(f"T-statistic: {t_stat}\nP-value: {p_value}")Nếu giá trị p-value nhỏ, điều này báo hiệu có sự khác biệt đáng kể giữa hai nhóm.
Phân Tích Phương Sai (ANOVA) Sử Dụng Scipy
ANOVA kiểm tra sự khác biệt giữa các trung bình của ba nhóm hoặc nhiều hơn. Ví dụ:
from scipy import stats
# Dữ liệu: điểm số của ba lớp học
class1_scores = [88, 92, 94, 95, 96]
class2_scores = [91, 92, 93, 94, 95]
class3_scores = [89, 90, 91, 92, 93]
# Thực hiện ANOVA
f_stat, p_value = stats.f_oneway(class1_scores, class2_scores, class3_scores)
print(f"F-statistic: {f_stat}\nP-value: {p_value}")Giá trị p-value thấp cho thấy ít nhất một cặp nhóm có sự khác biệt đáng kể về trung bình.
Kiểm Định Chi-Square Sử Dụng Scipy
Kiểm định chi-square thường được sử dụng để kiểm tra sự độc lập giữa các biến phân loại. Ví dụ:
from scipy.stats import chi2_contingency
# Bảng tần suất: Số học sinh thích môn học A, B, C trong hai lớp
data = [[30, 25, 20], [35, 30, 28]]
chi2, p_value, dof, expected = chi2_contingency(data)
print(f"Chi2 Statistic: {chi2}\nP-value: {p_value}")Trong ví dụ trên, nếu p-value thấp, chúng ta có thể bác bỏ giả thuyết không và kết luận rằng có sự phụ thuộc giữa lớp học và sở thích môn học.
Các ví dụ này chỉ là một phần của những gì scipy và statsmodels có thể thực hiện trong việc phân tích thống kê suy luận. Sự lựa chọn giữa các phương pháp này phụ thuộc vào dữ liệu và mục tiêu cụ thể của nghiên cứu.
Phân tích hồi quy
Phân tích hồi quy là một công cụ thống kê mạnh mẽ được sử dụng để mô hình hóa và phân tích mối quan hệ giữa các biến. Có hai loại hồi quy phổ biến: hồi quy tuyến tính và hồi quy logistic. Hồi quy tuyến tính được sử dụng khi biến phụ thuộc là liên tục và có mối quan hệ tuyến tính với biến độc lập. Trong khi đó, hồi quy logistic được sử dụng khi biến phụ thuộc là nhị phân.
Hồi Quy Tuyến Tính Sử Dụng Statsmodels và Scikit-learn
Statsmodels là một thư viện Python cho phép người dùng khám phá dữ liệu, ước lượng các mô hình thống kê và thực hiện kiểm định thống kê:
import statsmodels.api as sm import numpy as np # Giả sử X là biến độc lập và y là biến phụ thuộc X = np.random.rand(100, 1) # tạo dữ liệu giả y = X * 2 + np.random.normal(0, 0.1, size=(100, 1)) # mối quan hệ tuyến tính X = sm.add_constant(X) # thêm hằng số model = sm.OLS(y, X).fit() # Ước lượng mô hình print(model.summary()) # In bảng kết quả
Scikit-learn là một thư viện học máy phổ biến, hỗ trợ hồi quy tuyến tính với giao diện đơn giản:
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# Tạo dữ liệu và chia thành tập huấn luyện và kiểm tra
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
model = LinearRegression()
model.fit(X_train, y_train) # Huấn luyện mô hình
# Đánh giá mô hình
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f'MSE: {mse}')Hồi Quy Logistic Sử Dụng Scikit-learn
Hồi quy logistic thường được sử dụng để dự đoán xác suất của một sự kiện nhất định dựa trên một hoặc nhiều biến độc lập:
from sklearn.linear_model import LogisticRegression # Giả sử X là biến độc lập và y là biến phụ thuộc nhị phân model = LogisticRegression() model.fit(X_train, y_train) # Huấn luyện mô hình # Đánh giá mô hình y_pred = model.predict(X_test)
Đánh Giá Mô Hình
Đánh giá mô hình hồi quy tập trung vào việc xác định mức độ chính xác và độ tin cậy của mô hình:
- R-squared: Cho biết phần trăm biến thiên của biến phụ thuộc được giải thích bởi mô hình. Giá trị càng cao, mô hình càng tốt.
- AIC (Akaike Information Criterion) và BIC (Bayesian Information Criterion): Là các tiêu chí dựa trên thông tin, giúp so sánh các mô hình với nhau, với việc phạt những mô hình có quá nhiều tham số. Giá trị thấp hơn cho thấy mô hình tốt hơn.
Trực quan hóa dữ liệu
Trực quan hóa dữ liệu là một bước quan trọng trong quá trình phân tích thống kê, giúp tiết lộ thông tin sâu sắc và xu hướng không dễ nhận ra khi chỉ nhìn vào bảng số. Python cung cấp các thư viện mạnh mẽ như Matplotlib và Seaborn, cho phép tạo ra các biểu đồ trực quan đa dạng và đẹp mắt.
Biểu Đồ Phân Phối (Histogram, KDE)
- Histogram là biểu đồ thể hiện tần suất xuất hiện của dữ liệu trong các khoảng nhất định, hữu ích để nhìn thấy phân phối của dữ liệu.
- KDE (Kernel Density Estimate) là biểu đồ ước lượng mật độ xác suất, mềm mại hóa và thường được sử dụng cùng với histogram để hiểu rõ hơn về hình dạng của phân phối dữ liệu.
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
data = np.random.normal(size=100)
plt.figure(figsize=(10, 6))
sns.histplot(data, kde=True)
plt.title('Phân Phối Dữ Liệu')
plt.show()Biểu Đồ Hộp (Boxplot)
Biểu đồ hộp cung cấp cái nhìn tổng quan về phạm vi, phân vị và các giá trị ngoại lệ của dữ liệu, rất hữu ích để so sánh phân phối giữa các nhóm.
data = np.random.normal(size=(100, 3))
plt.figure(figsize=(10, 6))
sns.boxplot(data=data)
plt.title('Biểu Đồ Hộp')
plt.show()Scatter Plots và Regression Plots
- Scatter plots hiển thị mối quan hệ giữa hai biến, với mỗi điểm đại diện cho một quan sát.
- Regression plots bổ sung một đường hồi quy vào scatter plot, giúp nhìn rõ mối quan hệ tuyến tính giữa các biến.
x = np.random.normal(size=100)
y = x * 3 + np.random.normal(size=100)
plt.figure(figsize=(10, 6))
sns.regplot(x=x, y=y)
plt.title('Scatter Plot và Regression Line')
plt.show()Kết luận Thống kê Python
Do đó, trong hướng dẫn Thống kê Python này, chúng ta đã thảo luận về phép thử p-value, T-test, tương quan và KS với Python. Để kết luận, chúng tôi sẽ nói rằng giá trị p là một thước đo số cho bạn biết liệu dữ liệu mẫu có phù hợp với giả thuyết rỗng hay không. Tương quan là sự phụ thuộc lẫn nhau của các đại lượng biến thiên. Tuy nhiên, nếu có bất kỳ nghi ngờ nào về Thống kê Python, hãy hỏi trong tab nhận xét.


