Hồi quy tuyến tính là một trong những kỹ thuật thống kê cơ bản và mạnh mẽ nhất, được sử dụng rộng rãi trong việc dự đoán và dự báo các giá trị số. Một cách định nghĩa đơn giản, hồi quy tuyến tính là quá trình tìm ra đường thẳng tốt nhất phù hợp với một tập hợp các điểm dữ liệu, qua đó giúp chúng ta hiểu mối quan hệ giữa một biến phụ thuộc và một hoặc nhiều biến độc lập. Trong phương trình hồi quy tuyến tính cơ bản ( y = mx + c ), ( y ) là biến phụ thuộc mà chúng ta muốn dự đoán, ( x ) là biến độc lập, ( m ) là hệ số góc cho biết mức độ thay đổi của ( y ) khi ( x ) thay đổi, và ( c ) là hệ số chặn, cho biết giá trị của ( y ) khi ( x = 0 ).
Tầm quan trọng của hồi quy tuyến tính nằm ở khả năng ứng dụng của nó trong rất nhiều lĩnh vực thực tiễn. Từ kinh tế, y tế, khoa học dữ liệu, cho đến ngành công nghiệp và nghiên cứu khoa học, hồi quy tuyến tính giúp các nhà nghiên cứu và chuyên gia dự đoán các giá trị tương lai dựa trên dữ liệu quá khứ, phân tích xu hướng và mô hình hóa các mối quan hệ giữa các biến khác nhau.
Một ví dụ minh họa điển hình cho hồi quy tuyến tính có thể là trong ngành bất động sản, nơi mà giá của một ngôi nhà có thể được dự đoán dựa trên các yếu tố như diện tích, vị trí, số lượng phòng ngủ, và các tiện ích khác. Bằng cách thu thập dữ liệu từ các giao dịch bất động sản trước đó, một mô hình hồi quy tuyến tính có thể được xây dựng để dự đoán giá của một ngôi nhà dựa trên các đặc điểm của nó. Điều này giúp các nhà đầu tư, nhà phát triển và khách hàng có được cái nhìn sâu sắc hơn về thị trường, đồng thời hỗ trợ họ trong việc ra quyết định mua bán.
Định nghĩa về Linear Regression- Hồi quy tuyến tính
Linear Regression cố gắng mô hình hóa mối quan hệ giữa hai biến bằng cách điều chỉnh một phương trình tuyến tính với dữ liệu quan sát. Một biến được coi là biến giải thích và biến kia được coi là biến phụ thuộc. Ví dụ, một người lập mô hình có thể muốn liên hệ trọng lượng của các cá nhân với chiều cao của họ bằng cách sử dụng mô hình Linear Regression.
Trước khi cố gắng điều chỉnh mô hình tuyến tính với dữ liệu quan sát, trước tiên người lập mô hình phải xác định xem có hay không mối quan hệ giữa các biến quan tâm. Điều này không nhất thiết ngụ ý rằng một biến gây ra biến còn lại (ví dụ, điểm SAT cao hơn không gây ra điểm cao hơn ở đại học), nhưng có một số mối liên hệ đáng kể giữa hai biến. Biểu đồ phân tán có thể là một công cụ hữu ích trong việc xác định độ mạnh của mối quan hệ giữa hai biến.
Nếu dường như không có mối liên hệ nào giữa các biến giải thích và biến phụ thuộc được đề xuất (tức là biểu đồ phân tán không chỉ ra bất kỳ xu hướng tăng hoặc giảm nào), thì việc lắp mô hình Linear Regression với dữ liệu có thể sẽ không cung cấp một mô hình hữu ích. Một thước đo số có giá trị về mối liên kết giữa hai biến là hệ số tương quan, là giá trị từ -1 đến 1 cho biết mức độ liên kết của dữ liệu quan sát đối với hai biến.

Lý thuyết hồi quy tuyến tính
Ở tâm điểm của lý thuyết hồi quy tuyến tính là phương trình cơ bản ( y = mx + c ), một công thức toán học mô tả mối quan hệ giữa hai biến số. Trong phương trình này, ( y ) đại diện cho biến phụ thuộc, tức là giá trị mà chúng ta muốn dự đoán hoặc hiểu rõ hơn về sự ảnh hưởng của các biến khác lên nó. Biến ( x ), mặt khác, là biến độc lập, đại diện cho yếu tố hoặc biến số mà chúng ta cho rằng có ảnh hưởng đến ( y ).
Hệ số ( m ) trong phương trình, còn được gọi là hệ số góc, cho biết mức độ mạnh mẽ của mối quan hệ giữa ( x ) và ( y ). Giá trị này cung cấp thông tin về sự thay đổi của ( y ) với mỗi đơn vị thay đổi của ( x ). Ví dụ, nếu ( m = 2 ), điều này nghĩa là mỗi khi ( x ) tăng lên một đơn vị, ( y ) sẽ tăng lên hai đơn vị. Hệ số chặn ( c ), mặt khác, cho biết giá trị của ( y ) khi ( x = 0 ). Điều này cung cấp một điểm bắt đầu cho đường hồi quy trên trục y, cho phép chúng ta hiểu giá trị cơ bản của ( y ) ngay cả khi không có sự ảnh hưởng từ biến độc lập.
Để áp dụng hồi quy tuyến tính một cách hiệu quả, cần phải đảm bảo rằng dữ liệu phù hợp với một số giả định cơ bản. Đầu tiên, mối quan hệ giữa biến độc lập và biến phụ thuộc phải là tuyến tính, tức là dữ liệu có thể được mô tả tốt nhất bằng một đường thẳng. Thứ hai, phải có sự đồng nhất về phương sai, nghĩa là phương sai của các sai số (khoảng cách từ các điểm dữ liệu đến đường hồi quy) phải giữ nguyên không đổi ở mọi giá trị của biến độc lập. Cuối cùng, các sai số (hoặc dư lượng) của mô hình phải tuân theo phân phối chuẩn và là độc lập với nhau, không có sự tự tương quan. Đảm bảo rằng dữ liệu tuân thủ những giả định này giúp tăng cường tính chính xác và độ tin cậy của mô hình hồi quy tuyến tính.
Ứng dụng của Regression
Đường Linear Regression có phương trình dạng Y = a + bX, trong đó X là biến giải thích và Y là biến phụ thuộc. Hệ số góc của đường thẳng là b và a là giao điểm (giá trị của y khi x = 0).
Regression là một quá trình phổ biến được sử dụng trong nhiều ứng dụng thống kê trong thế giới thực. Có hai loại ứng dụng chính:
Dự đoán: Sau một loạt quan sát các biến, phân tích Regression đưa ra một mô hình thống kê cho mối quan hệ giữa các biến. Mô hình này có thể được sử dụng để tạo ra các dự đoán: cho trước hai biến x,x và y, y, mô hình có thể dự đoán các giá trị của yy cho các quan sát trong tương lai của x.x. Ý tưởng này được sử dụng để dự đoán các biến trong vô số tình huống, ví dụ: kết quả của các cuộc bầu cử chính trị, hành vi của thị trường chứng khoán, hoặc thành tích của một vận động viên chuyên nghiệp.
Tương quan: Mô hình được đưa ra bởi phân tích Regression thường sẽ phù hợp với một số loại dữ liệu tốt hơn những loại dữ liệu khác. Điều này có thể được sử dụng để phân tích mối tương quan giữa các biến và tinh chỉnh mô hình thống kê để kết hợp thêm các đầu vào: nếu mô hình mô tả rất tốt các tập con nhất định của các điểm dữ liệu, nhưng lại là một công cụ dự đoán kém cho các điểm dữ liệu khác, thì có thể hướng dẫn kiểm tra sự khác biệt giữa các loại điểm dữ liệu khác nhau để có thể giải thích. Loại ứng dụng này phổ biến trong các thử nghiệm khoa học, ví dụ: về tác dụng của một loại thuốc được đề xuất đối với bệnh nhân trong một nghiên cứu có đối chứng.
Least-Squares Regression
Phương pháp phổ biến nhất để điều chỉnh một đường Regression là phương pháp bình phương nhỏ nhất. Phương pháp này tính toán đường phù hợp nhất cho dữ liệu quan sát bằng cách giảm thiểu tổng bình phương của độ lệch dọc từ mỗi điểm dữ liệu đến đường (nếu một điểm nằm trên đường vừa khít thì độ lệch dọc của nó là 0). Bởi vì độ lệch đầu tiên được bình phương, sau đó được tổng hợp, không có sự hủy bỏ nào giữa các giá trị âm và dương.
Thí dụ
Tập dữ liệu “Ti vi, Bác sĩ và Kỳ vọng Cuộc sống”, trong số các biến số khác, số người trên mỗi máy truyền hình và số người trên mỗi bác sĩ ở 40 quốc gia.
Vì cả hai biến số có thể phản ánh mức độ giàu có ở mỗi quốc gia, nên có thể hợp lý để giả định rằng có một số mối liên hệ tích cực giữa chúng. Sau khi loại bỏ 8 quốc gia có giá trị bị thiếu khỏi tập dữ liệu, 32 quốc gia còn lại có hệ số tương quan là 0,852 cho số người trên mỗi máy thu hình và số người trên mỗi bác sĩ. Giá trị r² là 0,726 (bình phương của hệ số tương quan), cho thấy rằng 72,6% sự thay đổi trong một biến có thể được giải thích bởi biến kia.
Phương trình Regression là People.Phys. = 1019 + 56,2 People.Tel
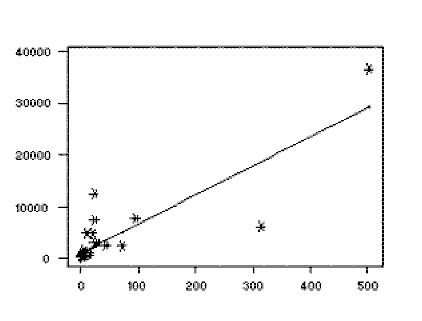
Để xem sự phù hợp của mô hình với dữ liệu quan sát, người ta có thể vẽ đường Regression tính toán trên các điểm dữ liệu thực tế để đánh giá kết quả. Đối với ví dụ này, với số lượng cá thể trên mỗi máy thu hình (biến giải thích) trên trục x và số lượng cá thể trên mỗi bác sĩ (biến phụ thuộc) trên trục y. Trong khi hầu hết các điểm dữ liệu được nhóm về phía góc dưới bên trái của biểu đồ (chỉ ra tương đối ít cá nhân trên mỗi máy thu hình và mỗi bác sĩ), có một vài điểm nằm xa nhóm dữ liệu chính. Những điểm này được gọi là ngoại lệ và tùy thuộc vào vị trí của chúng có thể có tác động lớn đến đường Regression (xem bên dưới).
Các quan sát ngoại lai và ảnh hưởng
Sau khi một đường Regression đã được tính toán cho một nhóm dữ liệu, một điểm nằm xa dòng (và do đó có giá trị thặng dư lớn) được gọi là giá trị ngoại lai. Những điểm như vậy có thể đại diện cho dữ liệu sai hoặc có thể chỉ ra một đường Regression kém phù hợp.

Nếu một điểm nằm xa dữ liệu khác theo hướng nằm ngang, nó được gọi là một quan sát có ảnh hưởng. Lý do cho sự khác biệt này là những điểm này có thể có tác động đáng kể đến độ dốc của đường Regression. Lưu ý, trong ví dụ trên, ảnh hưởng của việc loại bỏ quan sát ở góc trên bên phải của âm mưu:
Với quan sát có ảnh hưởng này bị loại bỏ, phương trình Regression bây giờ là
People.Phys = 1650 + 21.3 People.Tel
Mối tương quan giữa hai biến đã giảm xuống còn 0,427, điều này làm giảm giá trị r² xuống 0,182. Với quan sát có ảnh hưởng này bị loại bỏ, ít hơn 20% sự thay đổi về số người trên mỗi bác sĩ có thể được giải thích bởi số người trên mỗi máy truyền hình. Các quan sát có ảnh hưởng cũng được nhìn thấy có thể sử dụng mô hình mới và tác động của chúng cũng cần được điều tra.
Residuals
Khi một mô hình Regression đã phù hợp với một nhóm dữ liệu, việc kiểm tra các phần dư (độ lệch từ đường được điều chỉnh so với các giá trị quan sát được) cho phép người lập mô hình điều tra tính hợp lệ của giả định rằng tồn tại mối quan hệ tuyến tính. Việc vẽ biểu đồ phần dư trên trục y so với biến giải thích trên trục x cho thấy bất kỳ mối quan hệ phi tuyến tính nào có thể có giữa các biến hoặc có thể cảnh báo người lập mô hình để điều tra các biến ẩn.

Lurking Variables
Nếu các xu hướng phi tuyến tính có thể nhìn thấy được trong mối quan hệ giữa biến giải thích và biến phụ thuộc, thì có thể có các biến có ảnh hưởng khác cần xem xét. Một biến ẩn tồn tại khi mối quan hệ giữa hai biến bị ảnh hưởng đáng kể bởi sự hiện diện của biến thứ ba chưa được đưa vào nỗ lực mô hình hóa. Vì một biến số như vậy có thể là một yếu tố thời gian (ví dụ, ảnh hưởng của các chu kỳ chính trị hoặc kinh tế), một biểu đồ chuỗi thời gian của dữ liệu thường là một công cụ hữu ích trong việc xác định sự hiện diện của các biến tiềm ẩn.
Ngoại suy
Bất cứ khi nào mô hình Regression tuyến tính phù hợp với một nhóm dữ liệu, thì phạm vi của dữ liệu phải được quan sát cẩn thận. Việc cố gắng sử dụng một phương trình Regression để dự đoán các giá trị nằm ngoài phạm vi này thường không phù hợp và có thể mang lại các câu trả lời khó tin. Thực hành này được gọi là phép ngoại suy. Ví dụ, hãy xem xét một mô hình tuyến tính liên quan đến sự tăng cân theo độ tuổi của trẻ nhỏ. Áp dụng một mô hình như vậy cho người lớn, hoặc thậm chí thanh thiếu niên, sẽ là vô lý, vì mối quan hệ giữa tuổi và tăng cân không nhất quán cho tất cả các nhóm tuổi.
Xem thêm Data science
Những thách thức và vấn đề khi triển khai hồi quy tuyến tính
Trong quá trình xây dựng và triển khai mô hình hồi quy tuyến tính, các nhà phân tích thường gặp phải một số vấn đề thách thức có thể ảnh hưởng đến hiệu suất và độ chính xác của mô hình.
Đa cộng tuyến (Multicollinearity) xảy ra khi hai hoặc nhiều biến độc lập trong mô hình có mối quan hệ tuyến tính mạnh mẽ với nhau. Điều này làm cho việc xác định ảnh hưởng riêng biệt của mỗi biến độc lập lên biến phụ thuộc trở nên khó khăn và có thể làm tăng sai số của các ước lượng tham số. Để giải quyết vấn đề này, các phân tích viên có thể sử dụng phân tích yếu tố hoặc phân tích thành phần chính (PCA) để giảm đa cộng tuyến, hoặc loại bỏ một số biến độc lập có mối tương quan cao.
Dư thừa biến (Overfitting) là tình trạng mô hình quá phức tạp, phù hợp quá mức với dữ liệu huấn luyện đến mức nó mất khả năng tổng quát hóa trên dữ liệu mới. Overfitting có thể dẫn đến việc mô hình hiển thị hiệu suất tốt trên dữ liệu huấn luyện nhưng lại hoạt động kém trên dữ liệu kiểm tra hoặc dữ liệu thực tế. Một cách để ngăn chặn overfitting là sử dụng phương pháp như Lasso hoặc Ridge Regression, những phương pháp này thêm một thuật ngữ điều chuẩn vào hàm mất mát để kiểm soát độ phức tạp của mô hình.
Heteroscedasticity xảy ra khi phương sai của các sai số dự đoán thay đổi ở các giá trị khác nhau của biến độc lập. Điều này vi phạm giả định về sự đồng nhất của phương sai, một yêu cầu quan trọng trong hồi quy tuyến tính, và có thể dẫn đến ước lượng tham số không hiệu quả. Các kỹ thuật như chuyển đổi dữ liệu (logarithmic, square root transformation) hoặc sử dụng các mô hình hồi quy robust có thể giúp giảm thiểu vấn đề heteroscedasticity.
Để giải quyết những vấn đề này, việc phân tích kỹ lưỡng dữ liệu trước khi xây dựng mô hình là rất quan trọng. Sử dụng các biện pháp điều chỉnh như phân tích tương quan để phát hiện đa cộng tuyến, áp dụng kỹ thuật chọn và rút gọn biến để tránh overfitting, và kiểm tra các giả định về phương sai của sai số để xác định heteroscedasticity, là những bước quan trọng giúp tăng cường độ chính xác và độ tin cậy của mô hình hồi quy tuyến tính.
Đánh giá mô hình hồi quy tuyến tính
Đánh giá mô hình hồi quy tuyến tính là một bước quan trọng để hiểu mức độ chính xác và hiệu quả của mô hình trong việc dự đoán dữ liệu. Hệ số xác định (R^2) là một trong những chỉ số phổ biến nhất được sử dụng để đánh giá chất lượng của mô hình hồi quy. (R^2) đo lường tỷ lệ phần trăm biến thiên của biến phụ thuộc được giải thích bởi mô hình hồi quy. Giá trị của (R^2) nằm trong khoảng từ 0 đến 1, với giá trị gần 1 chỉ ra rằng mô hình giải thích một phần lớn biến thiên của dữ liệu và do đó có hiệu suất tốt.
Bên cạnh (R^2), các tiêu chí đánh giá khác như Mean Squared Error (MSE), Root Mean Squared Error (RMSE), và Mean Absolute Error (MAE) cũng rất quan trọng trong việc đánh giá mô hình. MSE là trung bình của bình phương các sai số giữa giá trị dự đoán và giá trị thực tế, cung cấp một cách đo lường tổng thể về khoảng cách giữa các giá trị dự đoán và thực tế. RMSE là căn bậc hai của MSE, mang lại độ lớn của sai số trong cùng một đơn vị với dữ liệu, làm cho nó dễ hiểu hơn. MAE là trung bình của giá trị tuyệt đối của các sai số, cung cấp một cái nhìn trực quan về mức độ lệch trung bình giữa dự đoán và thực tế.
Xem xét ví dụ sau: Giả sử bạn đã xây dựng một mô hình hồi quy tuyến tính để dự đoán giá nhà dựa trên diện tích. Sau khi áp dụng mô hình vào một tập dữ liệu kiểm tra, bạn tính được (R^2 = 0.85), điều này nghĩa là mô hình có thể giải thích 85% sự biến thiên của giá nhà dựa trên diện tích, một kết quả khá tốt. Tuy nhiên, bạn cũng tính được MSE là 20,000,000 (đơn vị giá nhà), RMSE là khoảng 4472.14, và MAE là 3500. Điều này cho thấy dù mô hình có khả năng giải thích tốt sự biến thiên của giá nhà, nhưng cũng có một khoảng lệch đáng kể giữa giá trị dự đoán và thực tế, với sai số trung bình khoảng 3500 đến 4472.14 đơn vị giá. Các chỉ số này giúp bạn hiểu rõ hơn về hiệu suất của mô hình và cung cấp hướng dẫn để cải thiện mô hình trong tương lai.
Hồi quy tuyến tính đa biến mở rộng
Hồi quy tuyến tính đa biến mở rộng khái niệm của hồi quy tuyến tính đơn biến bằng cách bao gồm nhiều biến độc lập hơn, cho phép mô hình hóa mối quan hệ giữa một biến phụ thuộc và hai hoặc nhiều biến độc lập. Trong hồi quy tuyến tính đa biến, phương trình hồi quy có dạng (Y = b_0 + b_1X_1 + b_2X_2 + … + b_nX_n), nơi (Y) là biến phụ thuộc mà chúng ta muốn dự đoán, (X_1, X_2, …, X_n) là các biến độc lập, và (b_0, b_1, …, b_n) là các hệ số hồi quy tương ứng với mỗi biến độc lập cũng như hệ số chặn.
Hồi quy tuyến tính đa biến cho phép phân tích ảnh hưởng của nhiều yếu tố độc lập lên một biến kết quả, làm tăng độ chính xác và tính toàn diện của mô hình. Ví dụ, trong một nghiên cứu về ảnh hưởng của các yếu tố như tuổi, giới tính, và chế độ ăn uống lên chỉ số cơ thể (BMI), hồi quy đa biến có thể giúp xác định mức độ ảnh hưởng của mỗi yếu tố khi đã kiểm soát ảnh hưởng của các yếu tố khác.
Tuy nhiên, hồi quy tuyến tính đa biến cũng đặt ra một số thách thức, bao gồm nguy cơ đa cộng tuyến giữa các biến độc lập, khiến cho việc ước lượng tham số trở nên khó khăn và giảm độ tin cậy của mô hình. Để giải quyết vấn đề này, có thể sử dụng các phương pháp như phân tích yếu tố hoặc loại bỏ các biến có mối tương quan cao. Ngoài ra, cần phải thực hiện kiểm tra độ phù hợp của mô hình, bao gồm kiểm tra giả định về sự độc lập và phân phối chuẩn của các dư lượng, cũng như sử dụng các tiêu chí đánh giá mô hình như (R^2) điều chỉnh, AIC, hoặc BIC để đánh giá mức độ phức tạp và hiệu suất của mô hình.
Bằng cách giải quyết những vấn đề này một cách cẩn thận, hồi quy tuyến tính đa biến có thể cung cấp cái nhìn sâu sắc và có giá trị về cách các biến độc lập tương tác với nhau và ảnh hưởng lên biến phụ thuộc, giúp ra quyết định dựa trên dữ liệu một cách chính xác và hiệu quả hơn.
Linear Regression trong Python
Linear Regression là một cách để mô hình hóa mối quan hệ giữa một phản hồi vô hướng (một biến phụ thuộc) với (các) biến giải thích (các biến độc lập). Tùy thuộc vào việc chúng ta có một hay nhiều biến giải thích, chúng tôi gọi nó là Linear Regression đơn giản và Linear Regression nhiều lần trong Python .
Để mô hình hóa các mối quan hệ, chúng tôi sử dụng các hàm dự báo tuyến tính với các tham số mô hình chưa biết; chúng tôi gọi các mô hình tuyến tính này bằng Python .
Ví dụ về Linear Regression trong Python
Hãy lấy một ví dụ đơn giản về Linear Regression trong Python.
import seaborn as sn
import matplotlib.pyplot as plt
sn.set(color_codes=True)
tips=sn.load_dataset('tips')
ax=sn.regplot(x='total_bill',y='tip',data=tips)
plt.show()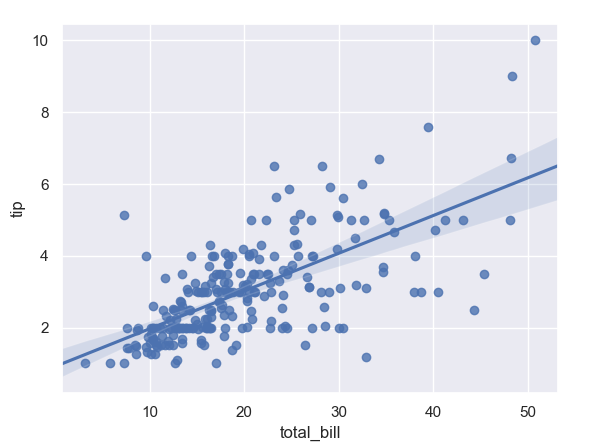
Làm thế nào để tùy chỉnh màu trong Python Linear Regression?
Bây giờ chúng ta hãy tô màu xanh lá cây.
import numpy as np np.random.seed(7) mean,cov=[3,5],[(1.3,.8),(.8,1.1)] x,y=np.random.multivariate_normal(mean,cov,77).T ax=sn.regplot(x=x,y=y,color='g') plt.show()
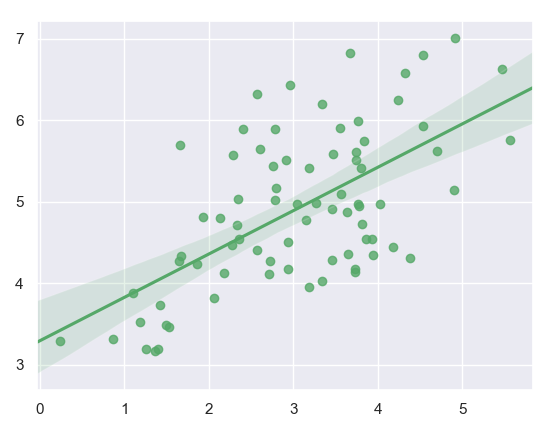
Vẽ đồ thị với chuỗi gấu trúc, điểm đánh dấu tùy chỉnh
Bây giờ, chúng ta sẽ sử dụng hai Chuỗi Pandas Python để vẽ biểu đồ Linear Regression Python.
import pandas as pd x,y=pd.Series(x,name='x'),pd.Series(y,name='y') ax=sn.regplot(x=x,y=y,marker='*')
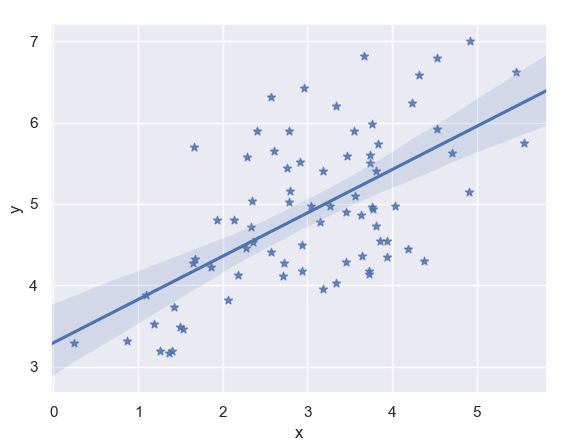
Đặt khoảng tin cậy
Để thiết lập khoảng tin cậy, chúng tôi sử dụng tham số ci. Khoảng tin cậy là một phạm vi giá trị làm cho giá trị của một tham số có thể nằm trong nó.
Hãy thảo luận về Bản đồ nhiệt Python
ax=sn.regplot(x=x,y=y,ci=68) plt.show()

Thêm Jitter
Bạn có thể thêm một số jitter theo hướng x hoặc y.
ax=sn.regplot(x='size',y='total_bill',data=tips,y_jitter=.1,color='g') plt.show()
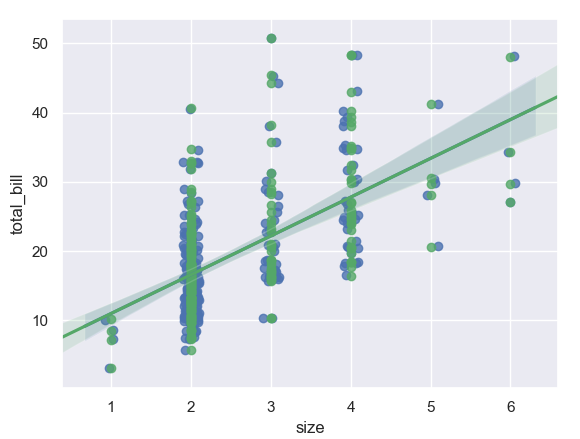
Lập kế hoạch với một biến số liên tục được chia thành các thùng rời rạc
Hãy sửa lại Biểu đồ Python
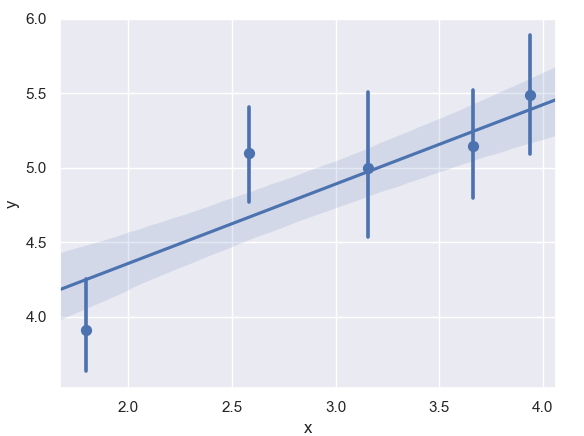
Hãy tạo 5 thùng và tạo biểu đồ.
ax=sn.regplot(x=x,y=y,x_bins=5) plt.show()
Kiểm tra Chi-Square là gì?
Đây là một thử nghiệm giả thuyết thống kê sử dụng phân phối chi bình phương làm phân phối lấy mẫu cho thống kê thử nghiệm khi chúng ta có giả thuyết rỗng thực sự. Nói cách khác, đó là một cách để đánh giá xem tập hợp các giá trị quan sát có phù hợp với các giá trị được mong đợi trong lý thuyết – mức độ phù hợp tốt như thế nào.
Bài kiểm tra cho chúng ta biết liệu, trong một hoặc nhiều danh mục, tần số dự kiến có khác biệt đáng kể so với tần số quan sát được hay không. Chúng tôi cũng viết nó là χ 2 kiểm tra. Trong thử nghiệm này, chúng tôi phân loại các quan sát thành các lớp loại trừ lẫn nhau. Giả thuyết vô hiệu cho chúng ta biết khả năng một quan sát rơi vào lớp tương ứng là bao nhiêu. Với thử nghiệm này, chúng tôi nhằm mục đích xác định khả năng một quan sát được thực hiện là bao nhiêu, đồng thời giả định rằng giả thuyết vô hiệu là đúng. Kiểm định Chi-Square này cho chúng ta biết liệu hai biến phân loại có phụ thuộc vào nhau hay không.
Ví dụ về Chi-Square trong Python
Hãy lấy một ví dụ.
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(0,10,100)
fig,ax=plt.subplots(1,1)
linestyles=['--','-.',':','-']
degrees_of_freedom=[1,3,7,5]
for df,ls in zip(degrees_of_freedom,linestyles):
ax.plot(x,stats.chi2.pdf(x,df),linestyle=ls)plt.xlim(0,7) plt.ylim(0,0.5)
Đoạn mã này vẽ các ô 4 dòng cho chúng ta-
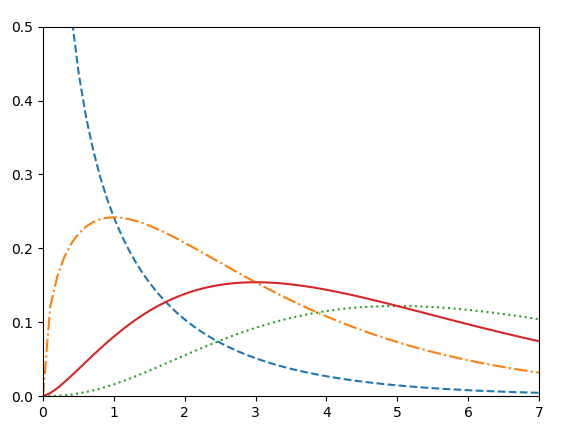
Ví dụ về Chi-Square trong Python
scipy.stats.chisquare
Điều này tính toán kiểm tra chi bình phương một chiều cho chúng tôi. Nó có cú pháp sau-
scipy.stats.chisquare(f_obs,f_exp=None,ddof=0,axis=0)
Hãy xem xét giả thuyết rỗng rằng dữ liệu phân loại được đề cập có các tần số đã cho. Phép thử Chi-square kiểm tra điều này.
Nó có các thông số sau-
- f_obs: array_like- Trong phần này, chúng tôi chỉ định các tần số quan sát được trong mọi danh mục
- f_exp: array_like, option- Điều này chứa các tần số mong đợi trong mọi danh mục; mỗi danh mục đều có khả năng như nhau theo mặc định
- ddof: int, option- Điều này giữ giá trị điều chỉnh ở bậc tự do cho giá trị p
- axis: int hoặc None, tùy chọn- Đây là trục của kết quả quảng bá của f_obs và f_exp; chúng tôi áp dụng thử nghiệm cùng với điều này
Nó có các giá trị trả về sau-
- chisq: float hoặc ndarray- Đây là thống kê kiểm tra chi bình phương
- p: float hoặc ndarray- Đây là giá trị p của bài kiểm tra
Bạn có biết về bản đồ địa lý Python
Đây là công thức cho tổng thống kê chi-bình phương
((quan sát-dự kiến) 2 / dự kiến)
Ví dụ về scipy.stats.chisquare
Hãy lấy một vài ví dụ đơn giản.
from scipy.stats import chisquare chisquare([6,8,6,4,2,2])
- Cung cấp tần số mong đợi
chisquare([6,8,6,4,2,2],f_exp=[6,6,6,6,6,8])
- Tần số quan sát 2D
data=np.array([[6,8,6,4,2,2],[12,10,6,11,10,12]]).T chisquare(data)
- Đặt trục thành Không có
chisquare(np.array([[6,8,6,4,2,2],[12,8,6,10,7,8]]),axis=None)
Tìm hiểu lô phân tán Python
chisquare(np.array([[6,8,6,4,2,2],[12,8,6,10,7,8]]).ravel())
- Thay đổi bậc tự do
chisquare([6,8,6,4,2,2],ddof=1)
- Tính toán giá trị p bằng cách phát thống kê chi bình phương với ddof
chisquare([6,8,6,4,2,2],ddof=[0,1,2])
Vì vậy, đây là tất cả trong Python Linear Regression. Hy vọng bạn thích giải thích của chúng tôi về Python Chi-Square Test.


