Suy luận trong First-Order logic được sử dụng để suy ra các dữ kiện hoặc câu mới từ các câu hiện có. Trước khi tìm hiểu quy tắc suy luận FOL, chúng ta hãy hiểu một số thuật ngữ cơ bản được sử dụng trong FOL.
Substitution:
Thay thế là một hoạt động cơ bản được thực hiện trên các thuật ngữ và công thức. Nó xảy ra trong tất cả các hệ thống suy luận theo First-Order Logic. Sự Substitution phức tạp khi có các bộ định lượng trong FOL. Nếu chúng ta viết F [a / x], thì nó đề cập đến việc Substitution một hằng số “a” thay cho biến “x”.
Lưu ý: First-Order logic có khả năng diễn đạt các dữ kiện về một số hoặc tất cả các đối tượng trong vũ trụ.
Equality:
First-Order logic không chỉ sử dụng vị ngữ và thuật ngữ để tạo câu nguyên tử mà còn sử dụng một cách khác, đó là đẳng thức trong FOL. Đối với điều này, chúng ta có thể sử dụng các ký hiệu Equality chỉ định rằng hai thuật ngữ đề cập đến cùng một đối tượng.
Ví dụ: Brother (John) = Smith.
Như trong ví dụ trên, đối tượng được Anh (John) giới thiệu tương tự với đối tượng được Smith giới thiệu. Biểu tượng Equality cũng có thể được sử dụng với sự phủ định để biểu thị rằng hai thuật ngữ không phải là các đối tượng giống nhau.
Ví dụ: ¬ (x = y) tương đương với x ≠ y.
Quy tắc suy luận FOL cho bộ định lượng
Là logic mệnh đề, chúng ta cũng có các quy tắc suy luận trong First-Order Logic, vì vậy sau đây là một số quy tắc suy luận cơ bản trong FOL:
- Universal Generalization
- Universal Instantiation
- Existential Instantiation
- Existential introduction
Universal Generalization
Tổng quát hóa phổ quát là một quy tắc suy luận hợp lệ nói rằng nếu tiền đề P (c) đúng với bất kỳ phần tử tùy ý c nào trong vũ trụ của diễn ngôn, thì chúng ta có thể có một kết luận là ∀ x P (x).
Nó có thể được biểu diễn dưới dạng:
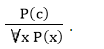
Quy tắc này có thể được sử dụng nếu chúng ta muốn chỉ ra rằng mọi phần tử đều có một thuộc tính giống nhau.
Trong quy tắc này, x không được xuất hiện dưới dạng một biến tự do.
Ví dụ: Hãy biểu diễn, P (c): “Một byte chứa 8 bit”, vì vậy đối với ∀ x P (x) “Tất cả các byte chứa 8 bit.”, Nó cũng sẽ đúng.
Universal Instantiation
Khởi tạo phổ quát còn được gọi là loại bỏ phổ quát hoặc UI là một quy tắc suy luận hợp lệ. Nó có thể được áp dụng nhiều lần để thêm các câu mới.
KB mới về mặt logic tương đương với KB trước đó.
Theo giao diện người dùng, chúng tôi có thể suy ra bất kỳ câu nào thu được bằng cách Substitution một thuật ngữ cơ bản cho biến.
Quy tắc giao diện người dùng nói rằng chúng ta có thể suy ra bất kỳ câu P (c) nào bằng cách thay một số hạng cơ bản c (một hằng số trong miền x) từ ∀ x P (x) cho bất kỳ đối tượng nào trong vũ trụ của diễn ngôn.
Nó có thể được biểu diễn dưới dạng:
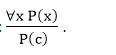
Ví dụ 1
NẾU “Mọi người đều thích kem” => ∀x P (x) thì chúng ta có thể suy ra rằng
“John thích kem” => P (c)
Ví dụ: 2
Hãy lấy một ví dụ nổi tiếng,
“Tất cả những vị vua tham lam đều là Ác ma.” Vì vậy, hãy để cơ sở kiến thức của chúng tôi chứa chi tiết này ở dạng FOL:
∀x vua (x) ∧ tham lam (x) → Ác ma (x),
Vì vậy, từ thông tin này, chúng tôi có thể suy ra bất kỳ câu nào sau đây bằng cách sử dụng Universal Instantiation:
- Vua (John) ∧ Tham lam (John) → Ác ma (John),
- Vua (Richard) ∧ Tham lam (Richard) → Ác độc (Richard),
- Vua (Cha (John)) ∧ Tham lam (Cha (John)) → Ác ma (Cha (John)),
Existential Instantiation
Khởi tạo hiện sinh còn được gọi là Loại bỏ hiện sinh, là một quy tắc suy luận hợp lệ trong First-Order Logic.
Nó chỉ có thể được áp dụng một lần để Substitution câu hiện sinh.
KB mới về mặt logic không tương đương với KB cũ, nhưng sẽ hài lòng nếu KB cũ được thỏa mãn.
Quy tắc này nói rằng người ta có thể suy ra P (c) từ công thức đã cho dưới dạng ∃x P (x) cho một ký hiệu hằng số mới c.
Hạn chế với quy tắc này là c được sử dụng trong quy tắc phải là một số hạng mới mà P (c) là đúng.
Nó có thể được biểu diễn dưới dạng:
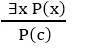
Ví dụ:
Từ câu đã cho: ∃x Crown (x) ∧ OnHead (x, John),
Vì vậy, chúng ta có thể suy ra: Crown (K) ∧ OnHead (K, John), miễn là K không xuất hiện trong cơ sở tri thức.
K được sử dụng ở trên là một ký hiệu hằng số, được gọi là hằng số Skolem.
Khởi tạo hiện sinh là một trường hợp đặc biệt của quá trình Skolemization.
Existential introduction
Giới thiệu hiện sinh còn được gọi là khái quát hiện sinh, là một quy tắc suy luận hợp lệ trong First-Order Logic.
Quy tắc này nói rằng nếu có một yếu tố c nào đó trong vũ trụ biểu hiện có thuộc tính P, thì chúng ta có thể suy ra rằng tồn tại một yếu tố nào đó trong vũ trụ có thuộc tính P.
Nó có thể được biểu diễn dưới dạng:

Ví dụ: Hãy nói rằng,
“Priyanka đạt điểm cao môn tiếng Anh.”
“Vì vậy, một người nào đó đã đạt điểm cao trong tiếng Anh.”
Quy tắc mô đun tổng quát Ponens
Đối với quy trình suy luận trong FOL, chúng tôi có một quy tắc suy luận duy nhất được gọi là Quy tắc suy luận tổng quát hóa mô-đun tổng quát. Nó là phiên bản nâng cấp của Modus ponens.
Mô đun tổng quát Ponens có thể được tóm tắt là, “P ngụ ý Q và P được khẳng định là đúng, do đó Q phải là Đúng.”
Theo Modus Ponens, đối với các câu nguyên tử pi, pi ‘, q. Khi có sự Substitution θ sao cho SUBST (θ, pi ‘,) = SUBST (θ, pi), nó có thể được biểu diễn như sau:
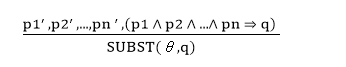
Ví dụ:
Chúng ta sẽ sử dụng quy tắc này cho Kings là ác, vì vậy chúng ta sẽ tìm thấy một số x sao cho x là vua và x là tham lam để chúng ta có thể suy ra rằng x là ác.
Here let say, p1' is king(John) p1 is king(x)
p2' is Greedy(y) p2 is Greedy(x)
θ is {x/John, y/John} q is evil(x)
SUBST(θ,q). 

