Sự suy luận
Trong trí tuệ nhân tạo, chúng ta cần những máy tính thông minh có thể tạo ra logic mới từ logic cũ hoặc bằng bằng chứng, vì vậy việc tạo ra kết luận từ bằng chứng và sự kiện được gọi là Suy luận.
Inference rules(suy luận quy tắc)
Các inference rules là các khuôn mẫu để tạo các đối số hợp lệ. Các inference rules được áp dụng để rút ra các bằng chứng trong trí tuệ nhân tạo và bằng chứng là một chuỗi các kết luận dẫn đến mục tiêu mong muốn.
Trong các inference rules, hàm ý giữa tất cả các kết nối đóng một vai trò quan trọng. Sau đây là một số thuật ngữ liên quan đến các inference rules:
- Implication: Nó là một trong những kết nối logic có thể được biểu diễn dưới dạng P → Q. Nó là một biểu thức Boolean.
- Converse: Nghĩa của hàm ý, có nghĩa là mệnh đề bên phải chuyển sang mệnh đề bên trái và ngược lại. Nó có thể được viết là Q → P.
- Contrapositive: Sự phủ định của converse được gọi là contrapositive, và nó có thể được biểu diễn dưới dạng ¬ Q → ¬ P.
- Inverse: Sự phủ định của hàm ý được gọi là nghịch đảo. Nó có thể được biểu diễn dưới dạng ¬ P → ¬ Q.
Từ thuật ngữ trên, một số câu lệnh ghép tương đương với nhau, chúng ta có thể chứng minh bằng cách sử dụng bảng chân trị:
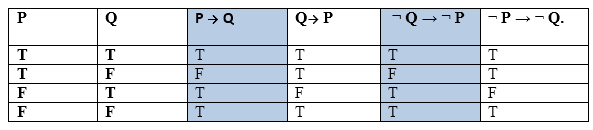
Do đó từ bảng chân lý trên, chúng ta có thể chứng minh rằng P → Q tương đương với ¬ Q → ¬ P, và Q → P tương đương với ¬ P → ¬ Q.
Các loại inference rules
Modus Ponens:
Quy tắc Modus Ponens là một trong những inference rules quan trọng nhất, và nó nói rằng nếu P và P → Q là đúng, thì chúng ta có thể suy ra rằng Q sẽ đúng. Nó có thể được biểu diễn dưới dạng:

Ví dụ:
Câu lệnh 1: “Nếu tôi buồn ngủ thì tôi đi ngủ” ==> P → Q
Câu lệnh-2: “Tôi buồn ngủ” ==> P
Kết luận: “Tôi đi ngủ.” ==> Q.
Do đó, chúng ta có thể nói rằng, nếu P → Q đúng và P đúng thì Q cũng đúng.
Bảng chứng minh bằng sự thật:

Modus Tollens:
Quy tắc Modus Tollens phát biểu rằng nếu P → Q đúng và ¬ Q đúng, thì ¬ P cũng đúng. Nó có thể được biểu diễn dưới dạng:
Câu lệnh 1: “Nếu tôi buồn ngủ thì tôi đi ngủ” ==> P → Q
Tuyên bố-2: “Tôi không đi ngủ.” ==> ~ Q
Câu lệnh-3: Suy ra rằng “Tôi không buồn ngủ” => ~ P
Bảng chứng minh bằng sự thật:

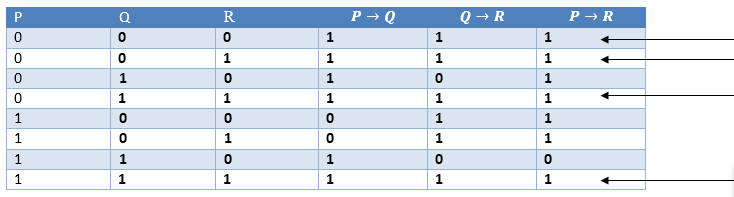
Hypothetical Syllogism
Quy tắc giả thuyết Syllogism phát biểu rằng nếu P → R là đúng bất cứ khi nào P → Q là đúng và Q → R là đúng. Nó có thể được biểu diễn dưới dạng ký hiệu sau:
Ví dụ:
Tuyên bố-1: Nếu bạn có chìa khóa nhà của tôi thì bạn có thể mở khóa nhà của tôi. P → Q
Tuyên bố-2: Nếu bạn có thể mở khóa nhà của tôi thì bạn có thể lấy tiền của tôi. Q → R
Kết luận: Nếu bạn có chìa khóa nhà của tôi thì bạn có thể lấy tiền của tôi. P → R
Chứng minh bằng bảng sự thật:
Disjunctive Syllogism
Disjunctive Syllogism phát biểu rằng nếu P∨Q là đúng, và ¬P là đúng, thì Q sẽ đúng. Nó có thể được biểu diễn dưới dạng:

Ví dụ:
Tuyên bố-1: Hôm nay là Chủ nhật hoặc Thứ Hai. ==> P∨Q
Tuyên bố-2: Hôm nay không phải là Chủ nhật. ==> ¬P
Kết luận: Hôm nay là thứ Hai. ==> Hỏi
Chứng minh bằng bảng sự thật:

Addition
Quy tắc Cộng là một trong những inference rules phổ biến, và nó nói rằng Nếu P đúng thì P∨Q sẽ đúng.

Ví dụ:
Tuyên bố: Tôi có một cây kem vani. ==> P
Tuyên bố-2: Tôi có kem sô cô la.
Kết luận: Tôi có kem vani hoặc sô cô la. ==> (P∨Q)
Chứng minh bằng Bảng Sự thật:

Simplification
Quy tắc đơn giản hóa phát biểu rằng nếu P∧ Q là đúng thì Q hoặc P cũng sẽ đúng. Nó có thể được biểu diễn dưới dạng:
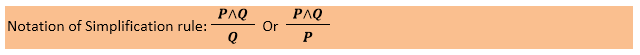
Chứng minh bằng Bảng Sự thật:

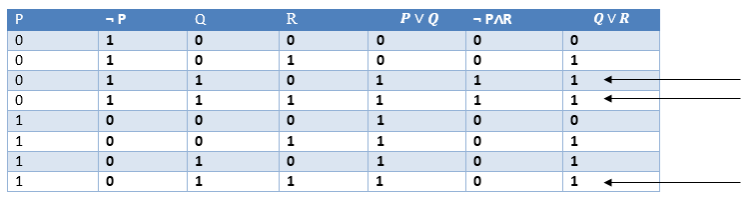
Resolution
Quy tắc phân giải phát biểu rằng nếu P∨Q và ¬ P∧R là đúng, thì Q∨R cũng sẽ đúng. Nó có thể được biểu diễn dưới dạng

Chứng minh bằng Bảng Sự thật: