Mạng Bayes, hay còn được biết đến với tên gọi Bayesian Networks, là một mô hình xác suất đồ thị giúp biểu diễn các mối quan hệ nguyên nhân giữa một tập hợp các biến và sử dụng lý thuyết xác suất Bayes để suy luận. Mạng này được cấu trúc dưới dạng một đồ thị có hướng, nơi các nút đại diện cho các biến ngẫu nhiên và các cạnh đại diện cho sự phụ thuộc có điều kiện giữa các biến. Điểm mạnh của mạng Bayes nằm ở khả năng mô hình hóa các quan hệ phức tạp và không xác định giữa các biến một cách trực quan và toán học.
Trong lĩnh vực học máy và trí tuệ nhân tạo, mạng Bayes đóng một vai trò quan trọng trong việc phát triển các hệ thống thông minh có khả năng học từ dữ liệu, dự đoán và ra quyết định dựa trên các nguyên tắc xác suất. Mạng này được sử dụng rộng rãi trong nhiều ứng dụng thực tế như chẩn đoán y khoa, hệ thống khuyến nghị, phát hiện gian lận và dự báo thời tiết.
Suy luận xác suất, nền tảng của mạng Bayes, là một phần không thể thiếu trong việc hiểu và sử dụng mô hình này. Suy luận xác suất cho phép chúng ta xác định xác suất của một sự kiện dựa trên thông tin có sẵn, giúp giải quyết các vấn đề quyết định trong điều kiện không chắc chắn. Thông qua quá trình này, mạng Bayes cung cấp một phương pháp mạnh mẽ và linh hoạt để phân tích và suy luận từ dữ liệu phức tạp, từ đó đưa ra những dự đoán và quyết định có cơ sở khoa học.
Cơ Sở Lý Thuyết
Lý thuyết xác suất Bayes, đặt tên theo nhà toán học Thomas Bayes, là một phần cốt lõi của thống kê và học máy, cung cấp một cơ sở toán học cho việc suy luận dựa trên xác suất. Công thức Bayes, nền tảng của lý thuyết này, mô tả mối quan hệ giữa xác suất có điều kiện và xác suất biên của các sự kiện ngẫu nhiên. Công thức này được biểu diễn như sau:
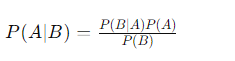
Trong đó:
- (P(A|B)) là xác suất có điều kiện của sự kiện A xảy ra khi biết sự kiện B đã xảy ra.
- (P(B|A)) là xác suất có điều kiện của sự kiện B xảy ra khi biết sự kiện A đã xảy ra.
- (P(A)) và (P(B)) là xác suất biên của sự kiện A và B tương ứng.
Trong mạng Bayes, công thức Bayes được sử dụng để suy luận ngược từ kết quả đến nguyên nhân, cho phép chúng ta cập nhật xác suất của một sự kiện dựa trên thông tin mới.
Mạng Bayes được cấu trúc dưới dạng một đồ thị có hướng, trong đó:
- Nút (Nodes) đại diện cho các biến ngẫu nhiên. Mỗi nút có thể tương ứng với một đặc trưng, một đối tượng, hoặc một khái niệm trong không gian vấn đề.
- Cạnh (Edges) biểu diễn mối quan hệ có điều kiện giữa các biến, cho phép mô hình hóa sự phụ thuộc và tương tác giữa chúng. Một cạnh từ nút A đến nút B chỉ ra rằng B có điều kiện phụ thuộc vào A.
- Bảng Xác Suất Có Điều Kiện (CPT – Conditional Probability Tables) kèm theo mỗi nút, mô tả xác suất của biến đó dưới các điều kiện khác nhau dựa trên giá trị của các biến mà nó phụ thuộc.
Mạng Bayes sử dụng cấu trúc này để mô hình hóa các quan hệ phức tạp và thực hiện suy luận xác suất, giúp chúng ta hiểu và dự đoán hành vi của các hệ thống phức tạp trong nhiều lĩnh vực khác nhau.
Suy luận mạng Bayes theo xác suất
Trong mạng Bayes, suy luận là quá trình xác định xác suất của một biến ngẫu nhiên dựa trên giá trị của các biến khác. Có hai loại suy luận chính: suy luận tiến (forward inference) và suy luận ngược (backward inference).
Suy Luận Tiến (Forward Inference)
Suy luận tiến diễn ra khi chúng ta sử dụng thông tin từ các nguyên nhân để dự đoán hậu quả. Trong bối cảnh của mạng Bayes, điều này nghĩa là chúng ta bắt đầu từ các biến gốc (root variables) và sử dụng thông tin từ chúng để dự đoán xác suất của các biến con sau đó trong mạng. Suy luận tiến thường được sử dụng để dự đoán kết quả của một sự kiện dựa trên các điều kiện hiện tại.
Suy Luận Ngược (Backward Inference)
Ngược lại với suy luận tiến, suy luận ngược bắt đầu từ kết quả và cố gắng xác định nguyên nhân. Trong mạng Bayes, nó liên quan đến việc sử dụng thông tin về các biến con để suy luận về xác suất của các biến gốc hoặc biến nguyên nhân. Suy luận ngược thường được sử dụng trong việc chẩn đoán, khi cần xác định nguyên nhân dựa trên các triệu chứng hoặc kết quả quan sát được.
Kỹ Thuật Suy Luận Phổ Biến
Suy Luận Chính Xác
Suy luận chính xác là quá trình tính toán chính xác xác suất của một biến trong mạng, dựa trên các giá trị đã biết của các biến khác. Các kỹ thuật suy luận chính xác bao gồm Enumeration, Variable Elimination, và Belief Propagation. Mặc dù chính xác, nhưng các phương pháp này có thể trở nên không khả thi về mặt tính toán khi mạng lớn và phức tạp.
Ví Dụ Minh Họa
Giả sử chúng ta có một mạng Bayes đơn giản với ba biến A, B, và C, nơi A là nguyên nhân của B và C. Chúng ta muốn tìm xác suất của B khi biết C = true. Sử dụng phương pháp Variable Elimination, chúng ta có thể thực hiện như sau:
- Xác định các biến cần loại bỏ, trong trường hợp này là A, vì chúng ta quan tâm đến xác suất của B.
- Tính toán xác suất kết hợp của B và C thông qua A, sau đó tổng hợp xác suất đó qua tất cả giá trị có thể của A.
- Tính xác suất cuối cùng của B bằng cách chuẩn hóa kết quả ở bước 2.
Dù ví dụ này khá giản đơn, nhưng nó minh họa cách tiếp cận cơ bản của phương pháp Variable Elimination trong việc giảm thiểu độ phức tạp của việc tính toán xác suất trong một mạng Bayes. Suy luận chính xác cung cấp cơ sở vững chắc để hiểu và sử dụng mạng Bayes một cách hiệu quả, dù với một số hạn chế về độ phức tạp tính toán.
Suy Luận Gần Đúng
Do hạn chế về mặt tính toán của suy luận chính xác, suy luận gần đúng được phát triển như một giải pháp thay thế. Các kỹ thuật suy luận gần đúng bao gồm Sampling Methods (ví dụ: Monte Carlo Sampling) và các phương pháp dựa trên Markov Chain Monte Carlo (MCMC). Những kỹ thuật này cung cấp một cách linh hoạt và hiệu quả để ước lượng xác suất trong các mạng Bayes phức tạp, mặc dù chúng không đảm bảo tính chính xác tuyệt đối như các phương pháp suy luận chính xác.
Việc chọn lựa giữa suy luận chính xác và suy luận gần đúng phụ thuộc vào kích thước và độ phức tạp của mạng, cũng như yêu cầu về độ chính xác và tài nguyên tính toán sẵn có.
Ví dụ Minh Họa
Xét một mạng Bayes đơn giản về dự đoán thời tiết, với các biến bao gồm nhiệt độ, lượng mưa và độ ẩm. Sử dụng phương pháp Gibbs Sampling trong MCMC, chúng ta có thể tạo ra một chuỗi các mẫu dựa trên phân phối xác suất có điều kiện của mỗi biến, cho phép chúng ta ước lượng xác suất của một ngày mưa mà không cần tính toán trực tiếp xác suất kết hợp của cả ba biến.
Suy luận gần đúng mở ra một cánh cửa mới cho việc xử lý và phân tích các mạng Bayes phức tạp, đem lại khả năng suy luận dựa trên dữ liệu lớn và phức tạp mà không bị giới hạn bởi rào cản về tính toán.
Thuật toán Structure Learning
Thuật toán Structure Learning giúp khám phá cấu trúc và tham số của Mạng Bayes (BN) từ dữ liệu. Các phương pháp này có thể xử lý dữ liệu cả rời rạc và liên tục, mở ra khả năng áp dụng trong nhiều ngành nghề khác nhau.
Các Thuật Toán Structure Learning Dựa Trên Ràng Buộc
Các thuật toán này tìm cách hiểu cấu trúc của mạng bằng cách xác định các ràng buộc giữa các biến. Một số ví dụ bao gồm:
- Grow-Shrink (GS): Phát hiện các biến độc lập có điều kiện để xác định cấu trúc mạng.
- Incremental Association Markov Blanket (IAMB) và các biến thể như Fast-IAMB và Inter-IAMB: Sử dụng quá trình tăng cường để xác định “chăn Markov” (một tập hợp các biến có ảnh hưởng trực tiếp đến biến mục tiêu).
Các Thuật Toán Structure Learning Dựa Trên Điểm Số
Những thuật toán này đánh giá các cấu trúc mạng khác nhau dựa trên một “điểm số” để xác định cấu trúc tối ưu. Ví dụ:
- Hill Climbing (HC) và Tabu Search (TS): Dùng các phương pháp tìm kiếm cục bộ để tối ưu hóa điểm số, với HC thử nghiệm các thay đổi nhỏ trong cấu trúc mạng và TS ngăn chặn việc quay lại trạng thái đã thăm trong quá khứ.
Các Thuật Toán Structure Learning Kết Hợp
Kết hợp các phương pháp dựa trên ràng buộc và điểm số để cải thiện khả năng tìm kiếm và chính xác của cấu trúc mạng.
- Max-Min Hill Climbing (MMHC): Kết hợp phát hiện Markov Blanket với Hill Climbing.
- Restricted Maximization (RSMAX2): Áp dụng các hạn chế dựa trên ràng buộc trong quá trình tối đa hóa điểm số.
Thuật Toán Khám Phá Cục Bộ
Nhằm tối ưu hóa cấu trúc mạng dựa trên quan sát cục bộ, giảm thiểu chi phí tính toán.
- Chow-Liu: Xây dựng cây phân phối xác suất gần đúng với tập dữ liệu.
- ARACNE và Min-Max Parents and Children (MMPC): Phát hiện các mối liên hệ quan trọng giữa các biến mà không cần khám phá toàn bộ không gian.
Bộ Phân Loại Mạng Bayes
Ứng dụng cụ thể của Structure Learning trong phân loại.
- Naive Bayes: Một mô hình đơn giản dựa trên giả định về sự độc lập giữa các biến đầu vào.
- Tree Augmented Naive Bayes (TAN): Mở rộng từ Naive Bayes bằng cách thêm cấu trúc cây giữa các biến để mô tả mối quan hệ phụ thuộc.
Thuật toán Structure Learning cung cấp cách tiếp cận linh hoạt và mạnh mẽ để xác định cấu trúc và tham số của Mạng Bayes, từ đó tối ưu hóa hiệu quả mô hình dựa trên


