Loss Function trong PyTorch

Loss Function trong PyTorch

Loss Function trong PyTorch là một hàm được sử dụng để tính toán sai số giữa các giá trị đầu ra được dự đoán và các giá trị thực tế của một mô hình học máy. Nó là một phần quan trọng của quá trình huấn luyện mô hình vì nó giúp mô hình cập nhật các trọng số và tham số để giảm thiểu sai số và tăng hiệu suất của mô hình.

PyTorch cung cấp một loạt các hàm Loss Function phổ biến như:

1. Mean Squared Error Loss (MSE Loss): Đây là hàm Loss Function đơn giản nhất và được sử dụng rộng rãi cho các bài toán hồi quy (regression). Nó tính toán sai số bình phương giữa các giá trị dự đoán và các giá trị thực tế.
2. Cross-Entropy Loss: Đây là hàm Loss Function phổ biến trong các bài toán phân loại (classification). Nó tính toán sai số giữa các giá trị dự đoán và các giá trị thực tế bằng cách sử dụng hàm log.
3. Binary Cross-Entropy Loss: Đây là một biến thể của hàm Cross-Entropy Loss được sử dụng cho các bài toán phân loại nhị phân (binary classification).
4. Categorical Cross-Entropy Loss: Đây là một biến thể khác của hàm Cross-Entropy Loss được sử dụng cho các bài toán phân loại đa lớp (multi-class classification).
5. Hinge Loss: Đây là hàm Loss Function được sử dụng cho các bài toán phân loại, đặc biệt là trong các bài toán phân loại đa lớp. Nó tính toán sai số bằng cách sử dụng hàm max(0, 1 – y * f(x)).

Mỗi hàm Loss Function sẽ được sử dụng tùy thuộc vào bài toán và loại mô hình học máy được sử dụng. PyTorch cũng cung cấp khả năng tạo ra hàm Loss Function tùy chỉnh, cho phép người dùng định nghĩa các hàm Loss Function riêng của họ cho các bài toán cụ thể.

• Hướng dẫn PyTorch
• Function trong JavaScript
• Function trong JavaScript: có thể bạn chưa biết
• Tạo Dataset của Perceptron Model trong Pytorch

Cách sử dụng Loss Function

Trong PyTorch, để sử dụng một hàm Loss Function, ta thường thực hiện các bước sau:

1. Import thư viện PyTorch:

import torch
import torch.nn as nn

2. Khởi tạo một đối tượng của hàm Loss Function cần sử dụng:

loss_fn = nn.MSELoss()

Ở đây, ta sử dụng hàm Mean Squared Error Loss (MSE Loss) làm ví dụ.

3. Tính toán loss bằng cách đưa dữ liệu đầu vào vào mô hình và tính toán sai số giữa các giá trị đầu ra và các giá trị thực tế:

y_pred = model(x)
loss = loss_fn(y_pred, y_true)

Ở đây, model là một đối tượng mô hình học máy được khởi tạo trước đó, x là dữ liệu đầu vào, y_true là các giá trị đầu ra thực tế, y_pred là các giá trị đầu ra được dự đoán bởi mô hình.

4. Sử dụng loss để cập nhật các trọng số và tham số của mô hình bằng cách tính toán gradient và sử dụng một thuật toán tối ưu hóa như stochastic gradient descent (SGD) để cập nhật các giá trị này:

optimizer.zero_grad()
loss.backward()
optimizer.step()

Ở đây, optimizer là một đối tượng tối ưu hóa được khởi tạo trước đó bằng cách sử dụng một thuật toán tối ưu hóa như SGD.

Các bước trên có thể được lặp lại nhiều lần để huấn luyện mô hình học máy. Mục đích của quá trình này là giảm thiểu sai số giữa các giá trị dự đoán và các giá trị thực tế, và đạt được hiệu suất tốt hơn của mô hình.

Các bài viết liên quan:

• Sử dụng Zendmap, NMap để tấn công và quét cổng
• Các gói phần mềm trong Pytorch
• Linear Regression trong Pytorch
• Gradient với PyTorch
• Number trong Dart

Thực nghiệm

Trong chủ đề trước, chúng tôi đã thấy rằng dòng không được khớp chính xác với dữ liệu của chúng tôi. Để làm cho nó phù hợp nhất, chúng tôi sẽ cập nhật các thông số của nó bằng cách sử dụng gradient descent, nhưng trước khi điều này, nó yêu cầu bạn biết về hàm Loss.

Vì vậy, mục tiêu của chúng tôi là tìm các tham số của một dòng phù hợp với dữ liệu này. Trong ví dụ trước của chúng tôi, hàm tuyến tính ban đầu sẽ gán tham số trọng số và thiên vị ngẫu nhiên cho dòng của chúng tôi với tham số sau.

Dòng này không thể hiện tốt dữ liệu của chúng tôi. Chúng tôi cần một số thuật toán tối ưu hóa sẽ điều chỉnh các thông số này dựa trên tổng sai số cho đến khi chúng tôi kết thúc với một dòng chứa các thông số phù hợp.

Bây giờ, làm thế nào để chúng ta xác định các thông số này?

Để hiểu rõ, chúng tôi giới hạn cuộc thảo luận của mình ở một điểm dữ liệu duy nhất.

Sai số được xác định bằng cách lấy giá trị y thực tế trừ đi dự đoán tại thời điểm đó.

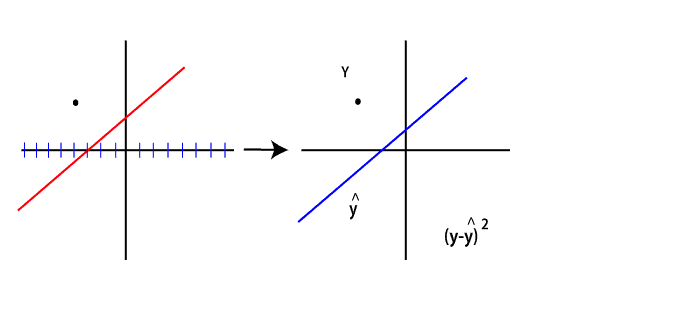
Dự đoán càng gần với giá trị, sai số càng nhỏ. Dự đoán như bạn đã biết có thể được viết dưới dạng

Tuy nhiên, chúng tôi đang đối phó với một dấu chấm duy nhất. Sao cho có thể vẽ vô hạn đường thẳng qua nó. Đối với điều này, chúng tôi loại bỏ sự thiên vị. Loại bỏ mức độ tự do bổ sung này ngay bây giờ và chúng tôi hủy bỏ nó bằng cách sửa giá trị thiên vị bằng 0.

Bây giờ, bất kỳ dòng nào mà chúng ta đang xử lý với dòng tối ưu sẽ có trọng số làm giảm sai số này càng gần 0 càng tốt. Bây giờ, chúng ta đang xử lý điểm (-3, 3) và đối với sự mất mát này, hàm sẽ dịch sang

Bây giờ, chúng ta tạo một bảng và thử giá trị khác nhau của A và xem giá trị nào cho chúng ta lỗi nhỏ nhất

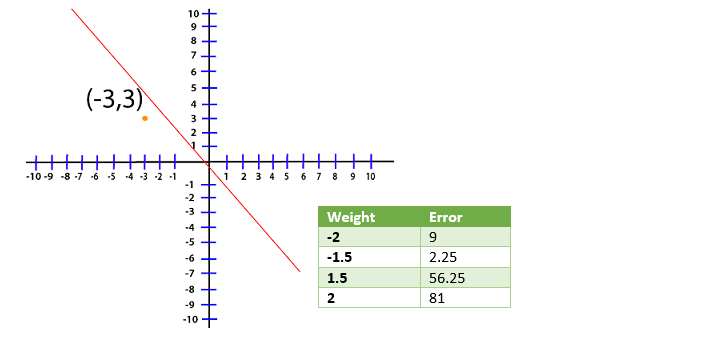
Chúng tôi vẽ biểu đồ các giá trị lỗi khác nhau cho các trọng số khác nhau trong cấp độ biểu đồ của tôi cho mục đích hình dung.

Trong trường hợp này, giá trị tối thiểu tuyệt đối tương ứng với trọng số của âm mà chúng ta biết cách đánh giá sai số tương ứng với phương trình tuyến tính của chúng ta.

Làm thế nào để chúng ta huấn luyện một người mẫu biết rằng trọng lượng này ngay tại đây? Đối với điều này, chúng tôi sử dụng Gradient Descent.