Resolution là một kỹ thuật chứng minh định lý được tiến hành bằng cách xây dựng các chứng minh bác bỏ, tức là chứng minh bằng các mâu thuẫn. Nó được phát minh bởi một nhà toán học John Alan Robinson vào năm 1965.
Giải pháp được sử dụng, nếu có nhiều phát biểu khác nhau được đưa ra, và chúng ta cần chứng minh kết luận của những phát biểu đó. Thống nhất là một khái niệm quan trọng trong chứng minh bằng nghị quyết. Resolution là một quy tắc suy luận có thể hoạt động hiệu quả trên dạng chuẩn liên hợp hoặc dạng mệnh đề.
Clause: Loại bỏ các nghĩa đen (một câu nguyên tử) được gọi là một mệnh đề. Nó còn được gọi là mệnh đề đơn vị.
Dạng thông thường liên kết: Một câu được biểu thị dưới dạng kết hợp của các mệnh đề được cho là dạng thông thường liên hợp hoặc CNF.
Các câu hỏi cạnh tranh về Cấu trúc bằng tiếng Hindi
Lưu ý: Để hiểu rõ hơn về chủ đề này, trước tiên hãy tìm hiểu FOL trong AI.
Quy tắc suy luận Resolution
Quy tắc phân giải cho logic bậc nhất chỉ đơn giản là một phiên bản nâng cấp của quy tắc mệnh đề. Resolution có thể giải quyết hai mệnh đề nếu chúng chứa các ký tự bổ sung, được giả định là được chuẩn hóa riêng biệt để chúng không có chung biến.
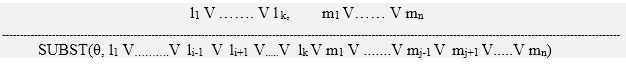
Trong đó li và mj là các chữ bổ sung cho nhau.
Quy tắc này còn được gọi là quy tắc phân giải nhị phân vì nó chỉ giải quyết đúng hai chữ.
Ví dụ:
Chúng tôi có thể giải quyết hai mệnh đề được đưa ra dưới đây:
[Animal (g (x) V Loves (f (x), x)] và [¬ Loves (a, b) V ¬Kills (a, b)]Trong đó hai từ bổ sung là: Yêu (f (x), x) và ¬ Yêu (a, b)
Các ký tự này có thể được hợp nhất với unifier θ = [a / f (x) và b / x], và nó sẽ tạo ra một mệnh đề giải quyết:
[Animal (g (x) V ¬ Kills (f (x), x)].Các bước giải quyết
- Chuyển đổi dữ kiện thành logic bậc nhất.
- Chuyển đổi các câu lệnh FOL thành CNF
- Phủ nhận tuyên bố cần chứng minh (chứng minh bằng mâu thuẫn)
- Vẽ đồ thị Resolution (thống nhất).
Để hiểu rõ hơn về tất cả các bước trên, chúng tôi sẽ lấy một ví dụ mà chúng tôi sẽ áp dụng giải pháp.
Ví dụ:
- John thích tất cả các loại thức ăn.
- Táo và rau là thực phẩm
- Bất cứ thứ gì ai ăn và không bị giết đều là thức ăn.
- Anil ăn đậu phộng và vẫn sống
- Harry ăn tất cả những gì Anil ăn.
- Chứng minh bằng cách giải quyết rằng:
- John thích đậu phộng.
Bước-1: Chuyển đổi sự kiện thành FOL
Trong bước đầu tiên, chúng ta sẽ chuyển đổi tất cả các câu lệnh đã cho thành logic bậc nhất của nó.

Bước 2: Chuyển đổi FOL thành CNF
Trong phân giải logic bậc nhất, cần phải chuyển đổi FOL thành CNF vì dạng CNF giúp cho việc chứng minh Resolution dễ dàng hơn.
- Loại bỏ tất cả hàm ý (→) và viết lại
- ∀x ¬ food (x) V alive(John, x)
- food (Apple) Λ food (vegetables)
- ∀x ∀y ¬ [eats (x, y) Λ ¬ killed(x)] V thức ăn (y)
- eats(Anil, Peanuts) Λ alive(Anil)
- ∀x ¬ eats (Anil, x) V eats(Harry, x)
- ∀x¬ [¬ killed(x)] V alive (x)
- ∀x ¬ alive (x) V ¬ killed(x)
- likes(John, Peanuts).
- Di chuyển phủ định (¬) vào trong và viết lại
- ∀x ¬ food (x) V likes(John, x)
- food (Apple) Λ food (vegetables)
- ∀x ∀y ¬ eats(x, y) V killed(x) V eats(y)
- eats(Anil, Peanuts) Λ alive(Anil)
- ∀x ¬ eats(Anil, x) V eats(Harry, x)
- ∀x ¬killed (x)] V alive(x)
- ∀x ¬ alive(x) V ¬ killed(x)
- likes(John, Peanuts).
- Đổi tên biến hoặc chuẩn hóa biến
- ∀x ¬ food (x) V likes(John, x)
- food (Apple) Λ food (vegetables)
- ∀y ∀z ¬ eats(y, z) V killed(y) V eats(z)
- eats(Anil, Peanuts) Λ alive(Anil)
- ∀w¬ eats(Anil, w) V eats (Harry, w)
- ∀g ¬killed (g)] V alive(g)
- ∀k ¬ alive(k) V ¬ killed(k)
- likes(John, Peanuts).
- Loại bỏ bộ định lượng tức thời hiện sinh bằng cách loại bỏ.
Trong bước này, chúng ta sẽ loại bỏ định lượng tồn tại ∃, và quá trình này được gọi là Skolemization. Nhưng trong bài toán ví dụ này vì không có định lượng tồn tại nên tất cả các câu lệnh sẽ được giữ nguyên trong bước này.
- Bỏ bộ định lượng Universal.
Trong bước này, chúng ta sẽ loại bỏ tất cả các định lượng phổ quát vì tất cả các câu lệnh không được định lượng một cách ngầm định nên chúng ta không cần nó.
- ¬ eats (x) V likes (John, x)
- Food (Apple)
- Food (vegetables)
- ¬ eats(y, z) V killed (y) V eats(z)
- Eats (Anil, Peanuts)
- alives(Anil)
- ¬ eats (Anil, w) V eats(Harry, w)
- Killed (g) V alive(g)
- ¬ killed (k) V ¬ Killed(k)
- likes(John, Peanuts).
Lưu ý: Các câu lệnh “food (Apple) Λ food (rau)” và “eat (Anil, Peanuts) Λ live (Anil)” có thể được viết thành hai câu riêng biệt.
- Phân phối kết hợp ∧ trên không kết hợp ¬.
Bước này sẽ không tạo ra bất kỳ thay đổi nào trong vấn đề này.
Bước 3: Phủ nhận tuyên bố để được chứng minh
Trong câu lệnh này, chúng tôi sẽ áp dụng phủ định cho các câu kết luận, sẽ được viết là ¬likes (John, Peanuts)
Bước 4: Vẽ đồ thị Resolution:
Bây giờ trong bước này, chúng ta sẽ giải quyết vấn đề bằng cây phân giải sử dụng phép thay thế. Đối với vấn đề trên, nó sẽ được đưa ra như sau:
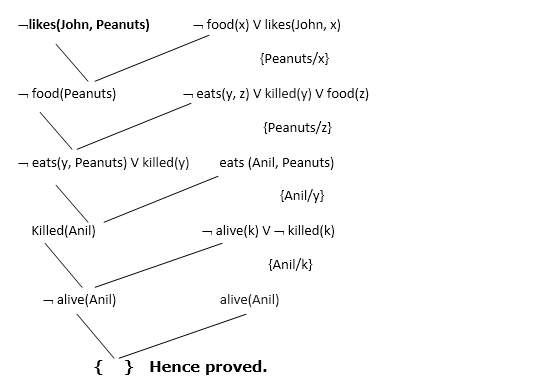
Do đó, phủ định của kết luận đã được chứng minh là hoàn toàn mâu thuẫn với tập hợp các phát biểu đã cho.
Giải thích về đồ thị Resolution
- Trong bước đầu tiên của biểu Resolution, likes (John, Peanuts) và likes (John, x) được giải quyết (bị hủy) bằng cách thay thế {Peanuts / x} và chúng ta chỉ còn lại ¬ food (Peanuts)
- Trong bước thứ hai của biểu Resolution, ¬ food(Hạt đậu các loại hạt), và food (z) được giải quyết (bị hủy) bằng cách thay thế {Peanuts / z}, và chúng ta chỉ còn lại ¬ eat (y, Peanuts) V killed (y).
- Trong bước thứ ba của biểu Resolution, eats (y, Peanuts) và eats(Anil, Peanuts) được giải quyết bằng cách thay thế {Anil / y}, và chúng ta còn lại với phần Killed (Anil).
- Trong bước thứ tư của biểu Resolution, Killed (Anil) và ¬ kill (k) được giải quyết bằng cách thay thế {Anil / k}, và chúng ta chỉ còn lại ¬ alive (Anil).
- Trong bước cuối cùng của đồ thị Resolution, alive(Anil) và alive(Anil) được giải quyết.


