Perceptron, một trong những khái niệm cơ bản nhất trong lĩnh vực mạng nơ-ron nhân tạo, được Frank Rosenblatt phát triển vào cuối những năm 1950. Ban đầu, Perceptron được thiết kế như một mô hình đơn giản của một tế bào thần kinh sinh học, có khả năng học dựa trên các tín hiệu đầu vào và đạt được kết quả đầu ra nhị phân. Mô hình này đã đánh dấu một bước tiến quan trọng trong việc mô phỏng quá trình ra quyết định của não bộ và mở đường cho sự phát triển của học máy và trí tuệ nhân tạo.
Ban đầu, Perceptron chỉ có một lớp (layer), đơn giản và chỉ phù hợp cho các tác vụ phân loại tuyến tính. Tuy nhiên, giới hạn này đã được vượt qua với sự phát triển của Multi-layer Perceptron (MLP). MLP bao gồm nhiều lớp, trong đó có các “hidden layers” – các lớp ẩn không trực tiếp nhìn thấy từ đầu vào hoặc đầu ra. Các mô hình này đã mở rộng khả năng của Perceptron, cho phép nó giải quyết các vấn đề phức tạp hơn, bao gồm cả phân loại phi tuyến và xấp xỉ hàm.
Trong bài viết này, chúng ta sẽ khám phá quá trình xây dựng và huấn luyện một Hidden Layer Perceptron sử dụng TensorFlow, một thư viện mạnh mẽ và linh hoạt trong lĩnh vực học máy và trí tuệ nhân tạo. Mục tiêu là cung cấp cho bạn đọc cái nhìn sâu sắc vào cách thức tạo ra một mô hình học sâu có khả năng xử lý các tác vụ phức tạp hơn so với mô hình Perceptron cổ điển. Qua đó, chúng ta sẽ hiểu rõ hơn về cơ chế hoạt động và tiềm năng ứng dụng của các mô hình học sâu trong thực tiễn.
Định nghĩa Hidden layer
Hidden Layer là một mạng nơ-ron nhân tạo là một lớp nằm giữa các lớp đầu vào và lớp đầu ra. Nơi các tế bào thần kinh nhân tạo tiếp nhận một tập hợp các đầu vào có trọng số và tạo ra đầu ra thông qua một chức năng kích hoạt. Nó là một phần của gần và thần kinh, trong đó các kỹ sư mô phỏng các loại hoạt động diễn ra trong não người.
Mạng nơ-ron ẩn được thiết lập trong một số kỹ thuật. Trong nhiều trường hợp, các đầu vào có trọng số được chỉ định ngẫu nhiên. Mặt khác, chúng được tinh chỉnh và hiệu chỉnh thông qua một quá trình được gọi là nhân giống ngược.
Tế bào thần kinh nhân tạo trong lớp ẩn của tế bào cảm thụ hoạt động như một tế bào thần kinh sinh học trong não – nó nhận các tín hiệu đầu vào xác suất và hoạt động trên chúng. Và nó chuyển đổi chúng thành một đầu ra tương ứng với sợi trục của nơ-ron sinh học.
Các lớp sau lớp đầu vào được gọi là ẩn vì chúng được phân giải trực tiếp đến đầu vào. Cấu trúc mạng đơn giản nhất là có một nơ-ron duy nhất trong lớp ẩn trực tiếp xuất ra giá trị.
Học sâu có thể đề cập đến việc có nhiều lớp ẩn trong mạng nơ-ron của chúng ta. Chúng rất sâu vì chúng sẽ chậm không thể tưởng tượng được để huấn luyện trong lịch sử, nhưng có thể mất vài giây hoặc vài phút để chuẩn bị bằng cách sử dụng các kỹ thuật và phần cứng hiện đại.
Cơ Sở Lý Thuyết của Multi-layer Perceptron
Cấu Trúc Cơ Bản của Multi-layer Perceptron
Multi-layer Perceptron (MLP) là một mô hình mạng nơ-ron nhân tạo, có cấu trúc bao gồm ba loại lớp chính:
- Input Layer: Lớp này chứa các nơ-ron đầu vào, mỗi nơ-ron đại diện cho một thuộc tính đặc trưng của dữ liệu. Nó hoạt động như cổng tiếp nhận thông tin, chuẩn bị cho quá trình xử lý tiếp theo trong mạng.
- Hidden Layers: Đây là lớp “ẩn” nằm giữa input layer và output layer. Các hidden layers chứa một hoặc nhiều lớp nơ-ron, không trực tiếp nhìn thấy từ bên ngoài. Chúng thực hiện các phép toán phức tạp trên dữ liệu đầu vào, mỗi lớp trích xuất và tinh chỉnh các đặc trưng khác nhau từ dữ liệu.
- Output Layer: Lớp này chứa nơ-ron đầu ra, cung cấp kết quả cuối cùng của mạng nơ-ron. Số lượng nơ-ron ở lớp này thường tương ứng với số lượng lớp hoặc giá trị đầu ra mong muốn (ví dụ: trong bài toán phân loại).
Chức Năng và Ý Nghĩa của Hidden Layers
Hidden layers là trái tim của một MLP, nơi diễn ra phần lớn các tính toán và học sâu. Mỗi hidden layer có thể được coi là một “cấp độ” của độ phức tạp hoặc trừu tượng hóa mà mạng có thể đạt được:
- Trích Xuất Đặc Trưng: Các hidden layers tự động học cách trích xuất và kết hợp các đặc trưng từ dữ liệu đầu vào, mỗi lớp tập trung vào các loại đặc trưng khác nhau.
- Độ Phức Tạp: Số lượng và kích thước của các hidden layers xác định khả năng của mạng trong việc xử lý các mô hình dữ liệu phức tạp. Nhiều hidden layers cho phép mạng “học sâu” hơn.
Các Hàm Kích Hoạt Trong Hidden Layers
Hàm kích hoạt (activation function) trong MLP đóng một vai trò quan trọng, giúp mô hình có khả năng học được các mối quan hệ phi tuyến tính. Một số hàm kích hoạt phổ biến bao gồm:
- ReLU (Rectified Linear Unit): Phổ biến nhất với tính năng không làm mất mát gradient trong quá trình lan truyền ngược, phù hợp cho các mô hình học sâu.
- Sigmoid: Chuyển đổi đầu vào thành giá trị đầu ra nằm trong khoảng từ 0 đến 1, thích hợp cho các bài toán phân loại nhị phân.
- Tanh (Hyperbolic Tangent): Tương tự như sigmoid nhưng sản xuất đầu ra trong khoảng từ -1 đến 1, giúp mô hình tạo ra dữ liệu được chuẩn hóa tốt hơn.
- Softmax: Thường được sử dụng trong lớp đầu ra của các mô hình phân loại, cung cấp xác suất của mỗi lớp.
Các hàm kích hoạt này giúp quyết định liệu một nơ-ron cụ thể có nên được “kích hoạt” hay không, dựa trên mức độ quan trọng của thông tin mà nó chứa. Việc chọn lựa hàm kích hoạt phù hợp phụ thuộc vào bản chất của dữ liệu và vấn đề cần giải quyết.
Xây Dựng Mô Hình Hidden Layer Perceptron
Trong việc xây dựng một Hidden Layer Perceptron sử dụng TensorFlow, ta cần xác định:
- Số Lượng Layers:
- Input Layer: Kích thước phụ thuộc vào số lượng đặc trưng của dữ liệu.
- Hidden Layers: Thông thường, 1-3 layers là đủ cho hầu hết các bài toán. Số lượng layers nhiều hơn giúp mô hình có khả năng học các mô hình phức tạp hơn nhưng cũng tăng rủi ro overfitting.
- Output Layer: Kích thước tùy thuộc vào số lượng lớp hoặc giá trị đầu ra (ví dụ: 1 node cho bài toán phân loại nhị phân).
- Số Lượng Nodes trong Mỗi Hidden Layer:
- Không có quy tắc cố định, nhưng một quy tắc thường gặp là sử dụng một số lượng nodes nằm giữa số lượng nodes của input layer và output layer.
- Hàm Kích Hoạt:
- Thông thường sử dụng ReLU cho các hidden layers.
- Sigmoid hoặc Softmax cho output layer, tùy thuộc vào loại bài toán (nhị phân hoặc đa lớp).
Hướng Dẫn Xây Dựng Mô Hình với TensorFlow
Sử dụng Keras API trong TensorFlow là cách đơn giản và hiệu quả để xây dựng mô hình. Dưới đây là ví dụ về cách xây dựng một mô hình Perceptron với một hidden layer:
import tensorflow as tf from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense # Xác định mô hình Sequential model = Sequential() # Thêm input layer và hidden layer đầu tiên model.add(Dense(10, input_shape=(num_input_features,), activation='relu')) # Thêm hidden layer thứ hai (nếu cần) # model.add(Dense(10, activation='relu')) # Thêm output layer model.add(Dense(num_output_classes, activation='sigmoid')) # Sử dụng 'softmax' cho bài toán phân loại đa lớp # Biên dịch mô hình model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
Trong ví dụ trên, num_input_features là số đặc trưng của dữ liệu đầu vào và num_output_classes là số lớp đầu ra (1 cho bài toán phân loại nhị phân, nhiều hơn cho bài toán phân loại đa lớp). Hàm Dense được sử dụng để tạo các layers, với tham số đầu tiên chỉ ra số lượng nodes trong layer và activation là hàm kích hoạt.
Lựa Chọn Số Lượng Hidden Layers và Nodes
- Hidden Layers: Bắt đầu với một hoặc hai hidden layers. Tăng số lượng layers nếu mô hình không đạt hiệu suất tốt.
- Số Nodes: Thử nghiệm với số lượng nodes tăng dần. Một số lượng nodes quá lớn có thể dẫn đến overfitting, trong khi quá ít có thể không đủ để học các mô hình phức tạp.
Mỗi bước trong quá trình thiết kế mô hình có thể yêu cầu điều chỉnh dựa trên kết quả đánh giá mô hình, dữ liệu cụ thể, và bài toán cần giải quyết.
Một lớp ẩn duy nhất sẽ xây dựng một mạng đơn giản.
Ví dụ về Hidden Layer Perceptron trong TensorFlow
Mã cho các lớp ẩn của perceptron được hiển thị bên dưới:
#Importing the essential modules in the hidden layer
import tensorflow as tf
import numpy as np
import mat
plotlib.pyplot as plt
import math, random
np.random.seed(1000)
function_to_learn = lambda x: np.cos(x) + 0.1*np.random.randn(*x.shape)
layer_1_neurons = 10
NUM_points = 1000
#Train the parameters of hidden layer
batch_size = 100
NUM_EPOCHS = 1500
all_x = np.float32(np.random.uniform(-2*math.pi, 2*math.pi, (1, NUM_points))).T
np.random.shuffle(all_x)
train_size = int(900)
#Train the first 700 points in the set x_training = all_x[:train_size]
y_training = function_to_learn(x_training)
#Training the last 300 points in the given set x_validation = all_x[train_size:]
y_validation = function_to_learn(x_validation)
plt.figure(1)
plt.scatter(x_training, y_training, c = 'blue', label = 'train')
plt.scatter(x_validation, y_validation, c = 'pink', label = 'validation')
plt.legend()
plt.show()
X = tf.placeholder(tf.float32, [None, 1], name = "X")
Y = tf.placeholder(tf.float32, [None, 1], name = "Y")
#first layer
#Number of neurons = 10
w_h = tf.Variable(
tf.random_uniform([1, layer_1_neurons],\ minval = -1, maxval = 1, dtype = tf.float32))
b_h = tf.Variable(tf.zeros([1, layer_1_neurons], dtype = tf.float32))
h = tf.nn.sigmoid(tf.matmul(X, w_h) + b_h)
#output layer
#Number of neurons = 10
w_o = tf.Variable(
tf.random_uniform([layer_1_neurons, 1],\ minval = -1, maxval = 1, dtype = tf.float32))
b_o = tf.Variable(tf.zeros([1, 1], dtype = tf.float32))
#building the model
model = tf.matmul(h, w_o) + b_o
#minimize the cost function (model - Y)
train_op = tf.train.AdamOptimizer().minimize(tf.nn.l2_loss(model - Y))
#Starting the Learning phase
sess = tf.Session() sess.run(tf.initialize_all_variables())
errors = []
for i in range(NUM_EPOCHS):
for start, end in zip(range(0, len(x_training), batch_size),\
range(batch_size, len(x_training), batch_size)):
sess.run(train_op, feed_dict = {X: x_training[start:end],\ Y: y_training[start:end]})
cost = sess.run(tf.nn.l2_loss(model - y_validation),\ feed_dict = {X:x_validation})
errors.append(cost)
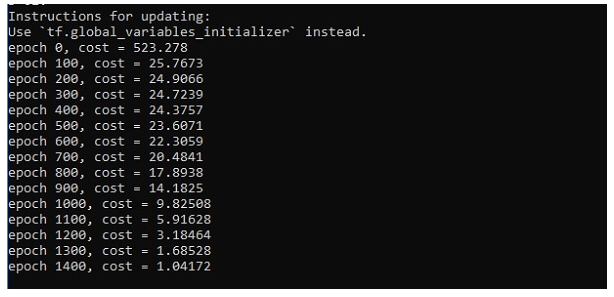
if i%100 == 0:
print("epoch %d, cost = %g" % (i, cost))
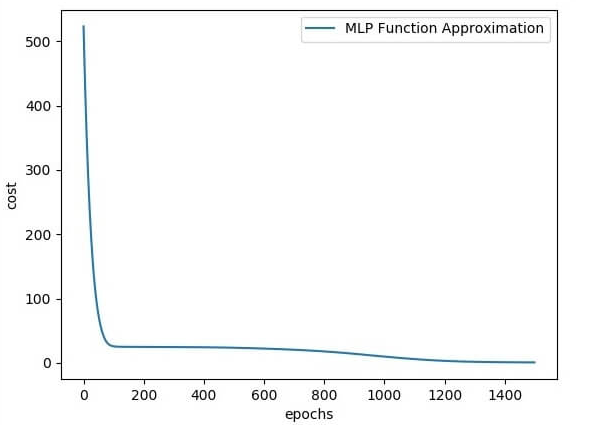
plt.plot(errors,label='MLP Function Approximation') plt.xlabel('epochs')
plt.ylabel('cost')
plt.legend()
plt.show()
Output
Sau đây là minh họa về xấp xỉ lớp chức năng-
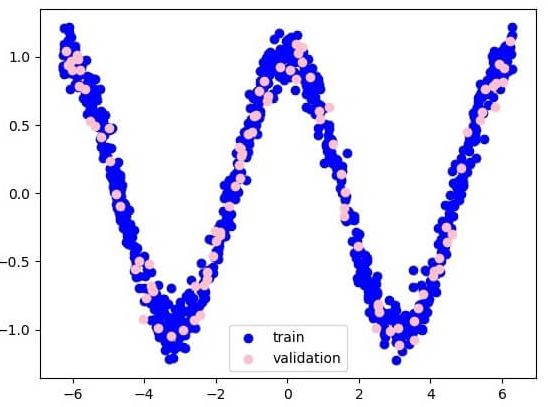
Ở đây hai dữ liệu được biểu diễn dưới dạng W.
Hai dữ liệu là: train và validation, được mô tả bằng các màu riêng biệt có thể nhìn thấy trong phần chú giải.
Ứng Dụng Thực Tiễn của Hidden Layer Perceptron
Nhận Dạng Hình Ảnh
Một trong những ứng dụng phổ biến nhất của Hidden Layer Perceptron là trong lĩnh vực nhận dạng hình ảnh. Mô hình Perceptron với nhiều hidden layers có khả năng học các đặc trưng phức tạp từ hình ảnh, từ đó có thể phân loại hoặc nhận dạng các đối tượng trong ảnh. Ví dụ, một mô hình MLP có thể được huấn luyện để nhận dạng các ký tự chữ và số trong ảnh, một ứng dụng hữu ích trong việc đọc biển số xe hoặc chuyển hóa văn bản ảnh thành văn bản số.
Phân Loại Văn Bản
Một lĩnh vực khác nơi Hidden Layer Perceptron thể hiện khả năng mạnh mẽ của mình là trong phân loại văn bản. Sử dụng mô hình này, các thuật toán có thể phân loại văn bản vào các danh mục khác nhau dựa trên nội dung, chẳng hạn như phân biệt email thường với email spam, hoặc phân loại các bài báo theo chủ đề. Điều này đặc biệt quan trọng trong quản lý thông tin và xử lý ngôn ngữ tự nhiên.
Dự Đoán và Phân Tích Dữ Liệu
Hidden Layer Perceptron cũng được sử dụng rộng rãi trong dự đoán và phân tích dữ liệu. Ví dụ, trong lĩnh vực tài chính, MLP có thể được sử dụng để dự đoán xu hướng thị trường chứng khoán dựa trên các dữ liệu lịch sử. Trong y tế, nó có thể giúp dự đoán sự phát triển của bệnh dựa trên các chỉ số sinh học của bệnh nhân.
Khám Phá Dữ Liệu và Phân Loại Tự Động
MLP cũng hữu ích trong việc khám phá dữ liệu, giúp phát hiện các mô hình và quan hệ không rõ ràng trong một tập dữ liệu lớn. Trong ngành công nghiệp, điều này có thể giúp trong việc phân loại tự động các sản phẩm dựa trên chất lượng hoặc đặc điểm sản xuất.
Tương Tác Người Máy
Cuối cùng, trong lĩnh vực tương tác người máy, MLP có thể giúp máy tính hiểu và phản ứng với các yêu cầu của con người một cách tự nhiên hơn, từ việc cải thiện khả năng trả lời tự động của chatbot đến việc cải thiện hiệu suất của các hệ thống trợ lý ảo.
Tất cả những ứng dụng này chỉ là một phần của tiềm năng mà Hidden Layer Perceptron mang lại, với khả năng học và phân tích dữ liệu phức tạp, mô hình này mở ra cánh cửa cho nhiều ứng dụng sáng tạo và giá trị trong thế giới thực.


