Trong lĩnh vực trí tuệ nhân tạo (AI), việc sử dụng các phương pháp xác suất và thống kê để xử lý dữ liệu và đưa ra quyết định là rất quan trọng. Định lý Bayes là một trong những công cụ mạnh mẽ nhất trong việc này. Định lý Bayes không chỉ giúp chúng ta hiểu và tính toán xác suất một cách hiệu quả mà còn có nhiều ứng dụng thực tiễn trong AI. Bài viết này sẽ giải thích chi tiết về định lý Bayes, cách thức hoạt động và các ứng dụng của nó trong trí tuệ nhân tạo.
Định lý Bayes là gì?
Định nghĩa
Định lý Bayes, được đặt theo tên của nhà toán học người Anh Thomas Bayes, là một phương pháp trong xác suất và thống kê để tính toán xác suất của một sự kiện dựa trên kiến thức trước đó về các điều kiện liên quan đến sự kiện đó. Công thức của định lý Bayes như sau:
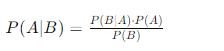
Trong đó:
- ( P(A|B) ) là xác suất của sự kiện A xảy ra khi biết sự kiện B đã xảy ra (gọi là xác suất hậu nghiệm).
- ( P(B|A) ) là xác suất của sự kiện B xảy ra khi biết sự kiện A đã xảy ra (gọi là xác suất có điều kiện).
- ( P(A) ) là xác suất tiên nghiệm của sự kiện A.
- ( P(B) ) là xác suất tiên nghiệm của sự kiện B.
Giải thích trực quan
Để hiểu rõ hơn về định lý Bayes, hãy xem xét một ví dụ đơn giản. Giả sử bạn có một bệnh viện và muốn tính xác suất một bệnh nhân bị bệnh A dựa trên kết quả xét nghiệm dương tính. Ta có các thông tin sau:
- Xác suất một người bị bệnh A là ( P(A) ).
- Xác suất kết quả xét nghiệm dương tính khi người đó bị bệnh A là ( P(B|A) ).
- Xác suất tổng thể của kết quả xét nghiệm dương tính là ( P(B) ).
Dựa vào định lý Bayes, chúng ta có thể tính toán xác suất bệnh nhân bị bệnh A khi biết kết quả xét nghiệm dương tính ( P(A|B) ).
Ứng dụng của định lý Bayes trong trí tuệ nhân tạo
Phân loại Bayes (Naive Bayes Classification)
Giới thiệu
Phân loại Bayes là một kỹ thuật học máy dựa trên định lý Bayes, được sử dụng rộng rãi trong các bài toán phân loại. Thuật toán Naive Bayes giả định rằng các đặc tính (features) là độc lập với nhau, điều này đơn giản hóa tính toán và làm cho thuật toán trở nên hiệu quả hơn.
Ứng dụng
- Lọc email spam: Naive Bayes được sử dụng để phân loại email thành thư rác hoặc thư hợp lệ dựa trên nội dung email.
- Phân loại văn bản: Naive Bayes được sử dụng để phân loại các tài liệu văn bản thành các danh mục khác nhau như tin tức, thể thao, giải trí.
- Nhận diện cảm xúc: Naive Bayes có thể được sử dụng để phân loại các bài đăng trên mạng xã hội hoặc đánh giá sản phẩm dựa trên cảm xúc tích cực hoặc tiêu cực.
Mạng Bayes (Bayesian Networks)
Giới thiệu
Mạng Bayes là một mô hình đồ thị xác suất đại diện cho tập hợp các biến ngẫu nhiên và các phụ thuộc có điều kiện giữa chúng thông qua một đồ thị không có chu trình (DAG). Mạng Bayes là công cụ mạnh mẽ trong việc mô hình hóa các hệ thống phức tạp và đưa ra các quyết định dựa trên xác suất.
Ứng dụng
- Chẩn đoán y tế: Mạng Bayes được sử dụng để chẩn đoán bệnh dựa trên các triệu chứng và kết quả xét nghiệm.
- Hệ thống khuyến nghị: Mạng Bayes có thể được sử dụng trong các hệ thống khuyến nghị để dự đoán sở thích của người dùng dựa trên hành vi và lịch sử của họ.
- Phân tích rủi ro: Mạng Bayes được sử dụng trong phân tích rủi ro tài chính và quản lý dự án để dự đoán các rủi ro và đưa ra các quyết định quản lý rủi ro.
Suy diễn Bayes (Bayesian Inference)
Giới thiệu
Suy diễn Bayes là quá trình cập nhật xác suất của một giả thuyết khi có thêm thông tin hoặc dữ liệu mới. Đây là một phương pháp quan trọng trong học máy và thống kê, giúp cải thiện các mô hình dựa trên dữ liệu mới.
Ứng dụng
- Học tăng cường (Reinforcement Learning): Trong học tăng cường, suy diễn Bayes được sử dụng để cập nhật các xác suất của các hành động và trạng thái dựa trên kinh nghiệm học tập.
- Dự báo chuỗi thời gian: Suy diễn Bayes được sử dụng để dự báo các chuỗi thời gian, chẳng hạn như giá cổ phiếu hoặc dữ liệu kinh tế, bằng cách cập nhật mô hình dự báo khi có thêm dữ liệu mới.
- Thử nghiệm A/B: Suy diễn Bayes có thể được sử dụng trong thử nghiệm A/B để đánh giá hiệu quả của các thay đổi trên website hoặc sản phẩm.
Những điều cần lưu ý khi sử dụng định lý Bayes
Giả định về độc lập
Naive Bayes giả định rằng các đặc tính (features) là độc lập với nhau, điều này không phải lúc nào cũng đúng trong thực tế. Mặc dù vậy, Naive Bayes vẫn hoạt động khá tốt trong nhiều trường hợp, nhưng bạn cần cẩn trọng khi áp dụng trong các bài toán mà các đặc tính có mối quan hệ mạnh với nhau.
Xác suất tiên nghiệm
Việc chọn xác suất tiên nghiệm ( P(A) ) có thể ảnh hưởng lớn đến kết quả của mô hình Bayes. Trong một số trường hợp, bạn cần có kiến thức chuyên môn để xác định xác suất tiên nghiệm chính xác hoặc sử dụng các phương pháp không chính thức như phân phối tiên nghiệm không xác định (non-informative priors).
Xử lý dữ liệu không đầy đủ
Mạng Bayes và các mô hình Bayes khác có thể xử lý dữ liệu không đầy đủ hoặc thiếu hụt, nhưng điều này có thể phức tạp và yêu cầu kỹ thuật chuyên sâu. Bạn cần có phương pháp xử lý dữ liệu phù hợp để đảm bảo tính chính xác của mô hình.
Kết luận
Định lý Bayes là một công cụ mạnh mẽ trong trí tuệ nhân tạo, cung cấp nền tảng cho nhiều phương pháp và ứng dụng quan trọng như phân loại, mạng Bayes và suy diễn Bayes. Hiểu rõ về định lý Bayes và cách áp dụng nó trong các bài toán thực tiễn có thể giúp bạn xây dựng các mô hình AI hiệu quả và chính xác hơn. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn chi tiết và rõ ràng về định lý Bayes và những ứng dụng của nó trong trí tuệ nhân tạo.
Tham khảo


