Machine learning: Thuật toán SVM

Machine Learning, một phần không thể thiếu trong lĩnh vực Trí tuệ nhân tạo (AI), đã mở ra một kỷ nguyên mới trong cách chúng ta xử lý dữ liệu và thu được thông tin hữu ích. Từ các ứng dụng như nhận dạng giọng nói, xử lý ngôn ngữ tự nhiên, đến phân tích xu hướng thị trường, Machine Learning đã trở thành công cụ cốt lõi giúp máy tính học hỏi từ dữ liệu và đưa ra các quyết định thông minh. Trong quá trình này, sự lựa chọn và sử dụng các thuật toán là yếu tố quan trọng quyết định đến hiệu suất và kết quả của mô hình.

Thuật toán SVM (Support Vector Machine) là một trong những thuật toán phổ biến và mạnh mẽ trong Machine Learning. Phát triển từ những năm 1960s và được hoàn thiện qua nhiều thập kỷ, SVM nổi bật với khả năng phân loại và hồi quy hiệu quả, đặc biệt trong các bài toán có không gian đặc trưng cao. Thuật toán này hoạt động dựa trên nguyên lý tìm ra mặt phẳng (hay hyperplane) tối ưu có thể phân chia dữ liệu thành các lớp với độ chính xác cao nhất.

Ứng dụng của SVM không chỉ giới hạn trong lĩnh vực học máy truyền thống như phân loại hình ảnh hay phân tích văn bản, mà còn mở rộng sang các lĩnh vực như sinh học tính toán, dự báo thị trường chứng khoán, và nghiên cứu y tế. Sự linh hoạt và hiệu suất cao của SVM khiến nó trở thành một công cụ quan trọng trong bất kỳ bộ công cụ nào của nhà khoa học dữ liệu.

Lịch sử và Phát triển của SVM

Lịch sử ra đời của SVM bắt đầu từ những năm 1960, với nền tảng lý thuyết đầu tiên được đặt ra bởi Vladimir Vapnik và Alexey Chervonenkis. Ban đầu, SVM được phát triển như một phương pháp trong lý thuyết học thống kê, với mục tiêu tạo ra một cách tiếp cận mới trong việc phân loại và dự đoán.

Những bước tiến quan trọng trong sự phát triển của SVM:

1. Những Năm Đầu (1960s – 1980s): Trong giai đoạn này, Vapnik và Chervonenkis đã xây dựng nên những nguyên tắc cơ bản của SVM, bao gồm khái niệm về “margin” và “hyperplane” trong không gian đặc trưng. Tuy nhiên, SVM chưa được chú ý nhiều trong cộng đồng học máy.
2. Sự Phát Triển và Nhận Diện (1990s): Thập kỷ 90 chứng kiến sự bùng nổ của SVM trong lĩnh vực học máy. Với việc giới thiệu các kỹ thuật như Kernel Trick, SVM trở nên mạnh mẽ và linh hoạt hơn, có khả năng xử lý dữ liệu phi tuyến tính.
3. Ứng Dụng Rộng Rãi (2000s – Hiện Nay): SVM đã trở thành một trong những thuật toán phổ biến và được ưa chuộng trong nhiều lĩnh vực ứng dụng khác nhau. Sự linh hoạt và hiệu suất cao của nó trong việc giải quyết các bài toán phân loại và hồi quy đã làm nổi bật SVM so với các thuật toán khác.
4. Sự phát triển của SVM không chỉ góp phần vào lĩnh vực Machine Learning, mà còn ảnh hưởng đến các ngành khoa học khác như thống kê, tối ưu hóa và logic. Với sự phát triển của công nghệ và sự gia tăng về khả năng tính toán, SVM tiếp tục phát triển và thích ứng, chứng tỏ sức mạnh và độ linh hoạt của nó trong một loạt các ứng dụng thực tế.

Nguyên Lý Cơ Bản của SVM

Support Vector Machine (SVM) là một thuật toán học máy mạnh mẽ, chủ yếu được sử dụng trong các bài toán phân loại (classification) và hồi quy (regression). Điểm nổi bật của SVM là khả năng tìm ra ranh giới quyết định (decision boundary) tối ưu giữa các lớp dữ liệu khác nhau.

Định nghĩa và Hoạt Động Cơ Bản:

Trong bài toán phân loại, SVM tìm cách tối đa hóa khoảng cách (margin) giữa các lớp dữ liệu. Nói cách khác, SVM tìm ra một mặt phẳng hay đường ranh giới (hyperplane) có khoảng cách xa nhất đến các điểm dữ liệu gần nhất của mỗi lớp, được gọi là các vector hỗ trợ (support vectors).

Mục tiêu là tối đa hóa margin này để tăng cường độ chính xác và khả năng tổng quát hóa của mô hình.

Không Gian Đặc Trưng (Feature Space) và Hyperplane:

SVM hoạt động bằng cách chuyển đổi dữ liệu vào không gian đặc trưng nhiều chiều để tìm ra hyperplane tối ưu. Điều này đặc biệt hữu ích trong các bài toán mà dữ liệu không tách biệt tuyến tính ở không gian ban đầu.

Một khía cạnh quan trọng của SVM là việc sử dụng các hàm nhân (kernel functions), như hàm nhân đa thức hoặc hàm nhân Gaussian (RBF). Các hàm nhân này cho phép SVM thực hiện phép biến đổi dữ liệu một cách hiệu quả vào không gian đặc trưng cao chiều mà không cần tính toán trực tiếp trong không gian đó. Điều này giúp SVM xử lý tốt các bài toán phức tạp với dữ liệu phi tuyến tính.

Nhờ vào sự linh hoạt và hiệu quả này, SVM đã trở thành một công cụ quan trọng trong Machine Learning, đặc biệt trong các bài toán phân loại và hồi quy mà dữ liệu không thể được tách biệt tuyến tính một cách rõ ràng.

Support vector machine (SVM) dùng để xây dựng một siêu mặt phẳng (hyperplane) để phân lớp (classify) tập dữ liệu thành hai lớp riêng biệt. Một siêu mặt phẳng là một hàm tương tự như phương trình đường thẳng y = ax + b. Trong thực tế, nếu ta chỉ cần phân lớp tập dữ liệu gồm hai feature siêu phẳng lúc này chính là một đường thẳng.

Về ý tưởng ban đầu thì SVM sử dụng thuật toán để ánh xạ dữ liệu ban đầu vào không gian nhiều chiều hơn. Khi ánh xạ tập dữ liệu sang nhiều chiều không gian từ đó SVM sẽ xem xét và chọn ra một siêu mặt phẳng phù hợp nhất để phân chia dữ liệu đó.

Các bài viết liên quan:

• Machine Learning? khái niệm cơ bản
• Data Collection trong nghiên cứu
• Xử lý dữ liệu không cân bằng
• Resampling(Lấy mẫu lại) dữ liệu không cân bằng
• Linear Regression- Hồi quy tuyến tính

Trong không gian hai chiều, ta biết rằng khoảng cách từ một điểm có tọa độ (x₀, y₀) tới một đường thẳng có phương trình w₁x + w₂y + b = 0 được xác định bởi công thức.

Trong không gian ba chiều, khoảng cách từ một điểm có tọa độ (x₀, y₀, z₀) tới một mặt phẳng có phương trình w₁x + w₂y + w₃z + b = 0 được xác định bởi công thức

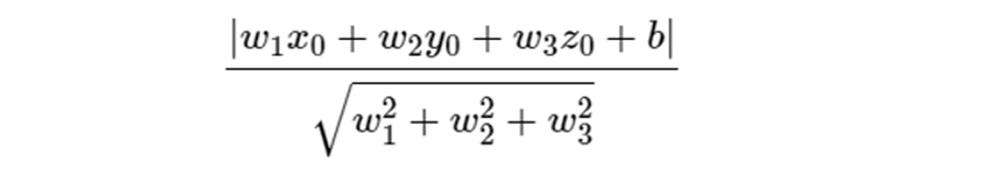
Nếu ta bỏ dấu giá trị tuyệt đối ở tử số, chúng ta có thể xác định điểm đó nằm về phía nào của đường thẳng hay mặt phẳng đang xét. Những điểm làm cho biểu thức trong dấu giá trị tuyệt đối mang dấu dương nằm về cùng một phía (gọi tạm đây là phía dương), những điểm làm cho biểu thức trong dấu giá trị tuyệt đối mang giá trị âm nằm về phía còn lại (gọi là phía âm). Những điểm nằm trên đường thẳng hoặc mặt phẳng sẽ làm cho tử số có giá trị bằng 0, tức khoảng cách từ điểm đang xét đến đường thẳng hoặc mặt phẳng bằng 0.

Xem thêm Kiểm tra lỗ hổng bảo mật HTTP Incoming Requests

Từ đây chúng ta có thể tổng quát lên không gian nhiều chiều. Khoảng cách từ một điểm (vector) có tọa độ x₀ đến một siêu mặt phẳng có phương trình w^Tx + b = 0 được xác định bởi công thức.

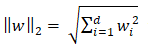
với d là số chiều không gian. Giả sử chúng ta có hai lớp khác nhau được mô tả bởi các điểm trong không gian nhiều chiều, bây giờ chúng ta cần tìm một mặt phẳng phân chia chính xác hai classes đó. Tức là tất cả các điểm thuộc một lớp sẽ nằm về cùng một phía của siêu mặt phẳng đó và ngược phía với toàn bộ các điểm thuộc class còn lại. Ta hãy xem xét hình dưới đây

Xem thêm Training model & testing SVM trong R

Trong các mặt phẳng đó đâu là mặt phẳng được phân chia tốt nhất, trong hình 3.5 ta thấy có hai mặt phẳng lệch về phía lớp có các điểm màu đỏ. Điều này sẽ gây ra việc lớp có các điểm màu đỏ sẽ cảm thấy bị hạn chế các điểm dữ liệu trên không gian so với lớp có các điểm màu xanh.

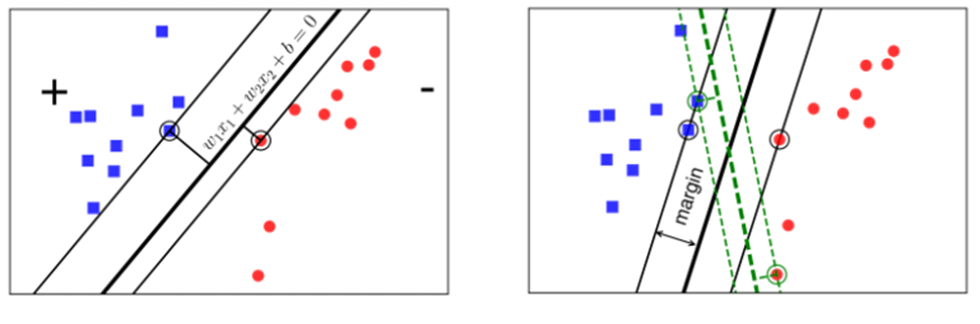
Nếu ta định nghĩa mức độ hạnh phúc của một lớp tỉ lệ thuận với khoảng cách gần nhất từ một điểm của lớp đó đến đường thẳng hoặc mặt phẳng thì lớp màu đỏ ở phía bên trái hình 3.6 sẽ không được hạnh phúc cho lắm vì khoảng cách từ điểm gần nhất của mỗi lớp đến đường hoặc mặt phẳng phân chia thì không đồng đều.

Vì vậy chúng ta cần tìm một đường hoặc mặt phẳng phân chia làm sao cho các điểm (vector) của hai lớp đến mặt phẳng là đồng đều. Tức là khoảng các điểm (vector) của lớp màu đỏ và lớp màu xanh gần nhất với đường thẳng hoặc mặt phẳng và cách đều các điểm (vector). Khoảng cách này được gọi mà margin.

Chúng ta nhìn khung bên phải hình 3.6 xét hai cách phân chia bởi đường nét liền màu đen và đường nét đứt màu xanh, rõ ràng ta thấy đường nét liền phân chia tốt hơn vì nó tạo ra margin rộng hơn đường nét màu xanh.

Việc margin rộng hơn sẽ mang lại hiệu ứng phân lớp tốt hơn vì việc phân chia giữa các lớp là rạch ròi hơn. Bài toán tối ưu trong SVM chính là bài toán đi tìm đường phân chia sao cho margin lớn nhất.

Giả sử ta có các cặp dữ liệu training set là (x₁, y₁), (x₂, y₂),…(x_N, y_N), với   , và y_i là nhãn của dữ liệu đó, d là số chiều của dữ liệu, N là số điểm dữ liệu, mỗi điểm dữ liệu được xác định bởi y_i = 1 (lớp 1) và  y_i = -1 (lớp 2). Để dễ hình dung ta nhìn hình phía dưới đây.

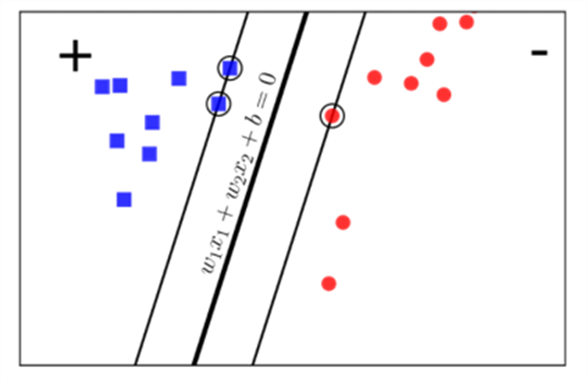
Các điểm (vector) ô vuông xanh thuộc lớp 1, các điểm tròn đỏ thuộc lớp 2 và mặt phân chia hai lớp ta có là  là mặt phẳng phân chia giữa hai lớp, lớp 1 nằm về phía dương và lớp 2 nằm về phía âm của mặt phân chia. Ta quan sát thấy một điểm quan trọng như sau với cặp dữ liệu (x_n, y_n) bất kỳ, khoảng cách từ điểm đó tới mặt phân chia là

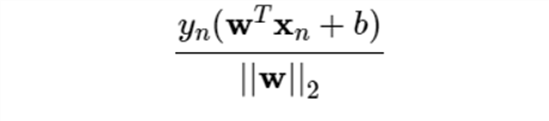
Ta có thể thấy nó gần giống công thức tính khoảng cách ở hình 3.8, thật chắc chúng như nhau. Khi ta định nghĩa lớp 1 là phía dương thì ta có  ngược lại ta có lớp 2 định nghĩa là phía âm nên có   do đó suy ra công thức chung đối với tất cả các điểm (vector) là  . Từ đó ta suy ra công thức đối với hình 3.9, ta nhìn hình dưới đây sẽ dễ hiểu hơn.

Đối với mỗi điểm dữ liệu ta có  từ đó ta có thể tính được margin bằng cách tính khoảng cách gần nhất từ một điểm đến mặt phẳng phân chia  . Bài toán SVM chính là bài toán tìm w và b sao cho margin này đạt giá trị lớn nhất.

Xem thêm Clustering- phân cụm trong R

SVM trong Phân Loại (Classification)

SVM và Bài Toán Phân Loại: Trong lĩnh vực phân loại, Support Vector Machine (SVM) được ưa chuộng nhờ khả năng xác định ranh giới rõ ràng giữa các lớp dữ liệu khác nhau. Điểm mạnh của SVM trong phân loại là khả năng tạo ra một hyperplane – một ranh giới quyết định – giúp tối đa hóa khoảng cách đến các điểm dữ liệu gần nhất của mỗi lớp, hay còn gọi là support vectors.

Cơ Chế Hoạt Động của SVM trong Phân Loại:

• SVM sẽ tìm cách xác định hyperplane sao cho khoảng cách từ hyperplane đến các điểm dữ liệu gần nhất (support vectors) là lớn nhất. Điều này tạo ra một lợi thế đáng kể: tối đa hóa margin giữa các lớp dữ liệu giúp tăng cường độ chính xác và khả năng tổng quát hóa của mô hình.
• Trong trường hợp dữ liệu không thể tách biệt tuyến tính, SVM sử dụng các hàm nhân (như RBF, đa thức) để biến đổi dữ liệu vào không gian đặc trưng cao chiều, nơi việc tìm ra một hyperplane phân chia là khả thi.

Ví Dụ Minh Họa:

• Giả sử chúng ta có một bài toán phân loại email thành ‘spam’ và ‘không spam’. SVM sẽ xác định ranh giới phân loại dựa trên các đặc trưng như tần suất xuất hiện của các từ khóa nhất định, số lượng liên kết trong email, vv.
• Dựa trên các đặc trưng này, SVM sẽ tạo ra một hyperplane phân chia hai lớp dữ liệu: một bên là ‘spam’, bên kia là ‘không spam’. Hyperplane này được xác định sao cho khoảng cách từ nó đến những email gần nhất ở mỗi lớp (các support vectors) là lớn nhất, nhằm đảm bảo rằng phân loại là chính xác và đáng tin cậy nhất có thể.

SVM trong phân loại là một công cụ mạnh mẽ, cung cấp phương pháp tiếp cận logic và hiệu quả cho việc tách biệt dữ liệu dựa trên các đặc trưng quan trọng. Sự linh hoạt và hiệu suất cao của nó trong nhiều tình huống khác nhau làm cho SVM trở thành một lựa chọn phổ biến trong nhiều ứng dụng Machine Learning.

SVM trong Hồi Quy (Regression)

Mặc dù SVM thường được biết đến với khả năng phân loại, nó cũng được ứng dụng hiệu quả trong lĩnh vực hồi quy, thông qua biến thể gọi là Support Vector Regression (SVR). SVR mở rộng nguyên lý cơ bản của SVM để xử lý các bài toán hồi quy, nơi mục tiêu là dự đoán một giá trị liên tục thay vì phân loại.

1. Cơ Chế Hoạt Động của SVR:
   • Trong SVR, thay vì tìm một hyperplane để phân chia dữ liệu thành các lớp, mục tiêu là tìm một hyperplane mà tối đa hóa khoảng cách đến các điểm dữ liệu gần nhất, đồng thời giữ cho khoảng cách từ các điểm dữ liệu đến hyperplane này nằm trong một lỗi chấp nhận được (epsilon).
   • Điều này tạo ra một dải “đường hầm” xung quanh hyperplane, nơi các điểm dữ liệu có thể nằm mà không bị coi là lỗi. Mục tiêu của SVR là tối thiểu hóa lỗi trong dải này.
2. Sự Khác Biệt giữa SVM trong Phân Loại và Hồi Quy:
   • Trong khi SVM phân loại tập trung vào việc tối đa hóa margin giữa các lớp và xác định ranh giới rõ ràng, SVR tập trung vào việc tối thiểu hóa lỗi dự đoán và tạo ra một mô hình dự đoán chính xác với một biên lỗi nhất định.
   • SVR không phân loại các điểm dữ liệu thành các lớp, mà dự đoán một giá trị liên tục dựa trên các đặc trưng của dữ liệu.

Ứng Dụng của SVR: SVR thích hợp cho các bài toán như dự đoán giá nhà, dự báo thời tiết, hoặc bất kỳ nhiệm vụ dự đoán nào mà giá trị đầu ra là liên tục và không rời rạc.

Ưu điểm và Nhược điểm của SVM

Thuật toán SVM, với sự linh hoạt và khả năng xử lý phức tạp của nó, mang lại nhiều ưu điểm nhưng cũng không thiếu những nhược điểm.

Ưu điểm của SVM:

1. Hiệu Quả trong Không Gian Đặc Trưng Lớn: SVM hoạt động rất tốt trong các không gian đặc trưng có số chiều lớn. Ngay cả trong trường hợp có số lượng đặc trưng lớn hơn số lượng mẫu, SVM vẫn có khả năng phân loại chính xác, làm cho nó trở thành lựa chọn lý tưởng cho nhiều bài toán phức tạp.
2. Hiệu Suất Cao trong Nhiều Trường Hợp: SVM được biết đến với khả năng tạo ra ranh giới quyết định chính xác, đặc biệt khi các lớp dữ liệu không tách biệt hoàn toàn. Sự tinh tế trong việc tối ưu hóa margin giúp SVM đạt được hiệu suất cao trong nhiều tình huống khác nhau.

Nhược điểm của SVM:

1. Khó Khăn trong Việc Lựa Chọn và Tinh Chỉnh Tham Số: Việc lựa chọn hyperparameters phù hợp, như tham số C (điều chỉnh trade-off giữa lỗi phân loại và mức độ mịn của ranh giới quyết định), và các tham số của hàm nhân, đòi hỏi kinh nghiệm và thử nghiệm. Quá trình này có thể phức tạp và tốn thời gian.
2. Giới Hạn ở Quy Mô Dữ Liệu Lớn: Khi xử lý bộ dữ liệu có quy mô lớn, SVM có thể trở nên không hiệu quả về mặt tính toán. Đặc biệt, việc sử dụng các hàm nhân trong SVM có thể dẫn đến việc tăng đáng kể trong việc tính toán và yêu cầu bộ nhớ, làm chậm quá trình huấn luyện và dự đoán.