Single Layer Perceptron là một trong những mô hình cơ bản nhất trong lịch sử học máy và trí tuệ nhân tạo. Được phát triển bởi Frank Rosenblatt vào năm 1957, Perceptron ban đầu là một mô hình thần kinh nhân tạo đơn giản, mô phỏng cách mà một tế bào thần kinh sinh học phản ứng với các kích thích từ bên ngoài. Perceptron này chỉ gồm một lớp duy nhất gồm nhiều nơ-ron, mỗi nơ-ron nhận đầu vào và đưa ra đầu ra dựa trên một hàm kích hoạt nhất định.
Trong cấu trúc của Single Layer Perceptron, đầu vào thường được biểu diễn dưới dạng một vectơ các đặc trưng, và mỗi nơ-ron trong Perceptron này sẽ thực hiện một tổng trọng số của các đặc trưng đó, sau đó áp dụng một hàm kích hoạt (thường là một hàm bước như hàm Heaviside) để đưa ra dự đoán cuối cùng. Mô hình này chủ yếu được sử dụng trong các tác vụ phân loại đơn giản, nơi nó cố gắng phân tách dữ liệu thành hai lớp khác nhau.
Trong bài viết này, mục tiêu chính là hướng dẫn cách xây dựng và sử dụng một Single Layer Perceptron sử dụng TensorFlow, một trong những thư viện học máy phổ biến và mạnh mẽ nhất hiện nay. Chúng ta sẽ đi qua từng bước từ việc cài đặt TensorFlow, xây dựng mô hình Perceptron, huấn luyện nó trên một tập dữ liệu, và cuối cùng là đánh giá hiệu suất của mô hình. Bài viết này sẽ cung cấp kiến thức cơ bản và đủ để bắt đầu với việc sử dụng TensorFlow cho học máy, đặc biệt là với những người mới bắt đầu trong lĩnh vực này.
Định nghĩa về Single Layer Perceptron
Single Layer Perceptron, một trong những khái niệm cơ bản nhất trong lĩnh vực mạng nơ-ron nhân tạo, là mô hình đơn giản nhất của một mạng nơ-ron. Được phát triển vào những năm 1950s bởi Frank Rosenblatt, Single Layer Perceptron thể hiện một cố gắng ban đầu trong việc mô phỏng hoạt động của tế bào thần kinh sinh học trong não bộ con người.
Cấu trúc của Single Layer Perceptron bao gồm một lớp đơn (single layer) của các nơ-ron, mà mỗi nơ-ron nhận các tín hiệu đầu vào và tạo ra một tín hiệu đầu ra. Mỗi nơ-ron trong lớp này thực hiện một phép toán tổng trọng số của các đầu vào, sau đó áp dụng một hàm kích hoạt – thường là một hàm bước như hàm Heaviside – để quyết định đầu ra cuối cùng. Nếu tổng trọng số vượt qua một ngưỡng cố định, nơ-ron sẽ “kích hoạt” và đưa ra đầu ra là 1 (hoặc -1); ngược lại, nó sẽ không kích hoạt và đưa ra đầu ra là 0.
Perceptron đơn lớp thường được sử dụng trong các tác vụ phân loại đơn giản, nơi nó cố gắng phân tách dữ liệu thành hai lớp khác biệt. Mô hình này hoạt động tốt với dữ liệu có thể được phân loại tuyến tính, nhưng có những hạn chế trong việc giải quyết các vấn đề phức tạp hơn, không tuyến tính. Điểm yếu này dẫn đến việc phát triển các mô hình mạng nơ-ron phức tạp hơn, như Multi-layer Perceptron, có khả năng học các mô hình dữ liệu phức tạp hơn.
Perceptron sử dụng hàm bước trả về +1 nếu tổng trọng số của đầu vào của nó là 0 và -1.
Hàm kích hoạt được sử dụng để ánh xạ đầu vào giữa giá trị cần thiết như (0, 1) hoặc (-1, 1).
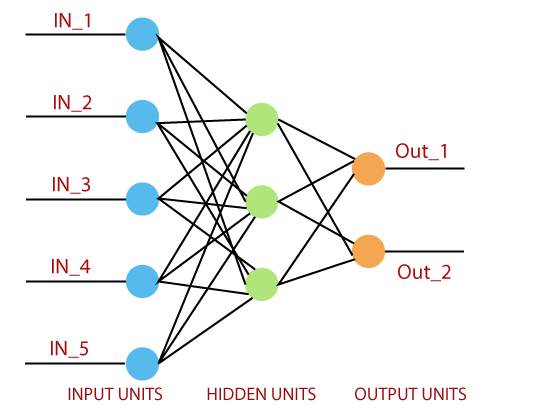
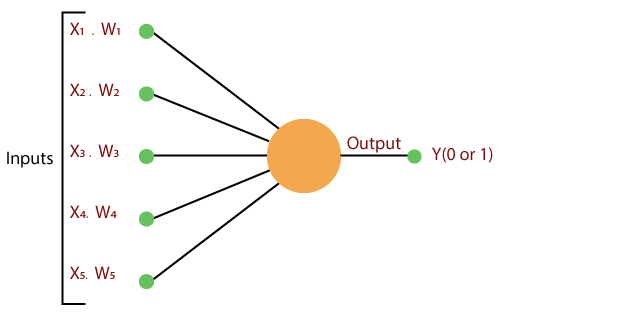
Một mạng nơ-ron thông thường trông giống như sau:
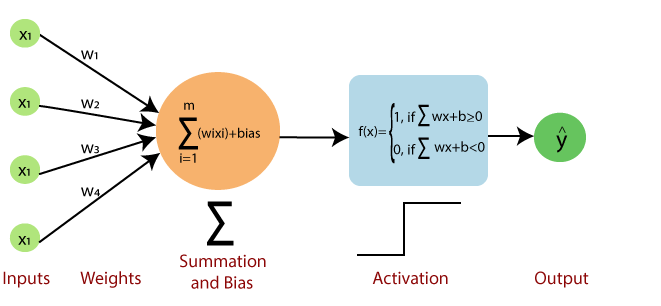
Cơ Sở Lý Thuyết về Perceptron
Perceptron là một mô hình mạng nơ-ron nhân tạo đơn giản, được thiết kế để mô phỏng cách mà một tế bào thần kinh sinh học xử lý thông tin. Cấu trúc cơ bản của Perceptron bao gồm:
- Đầu Vào (Inputs): Các giá trị đầu vào đại diện cho các đặc trưng của dữ liệu. Mỗi đầu vào có một trọng số riêng biệt, phản ánh tầm quan trọng của đặc trưng đó trong việc đưa ra quyết định.
- Tổng Trọng Số (Weighted Sum): Perceptron tính toán tổng trọng số của các đầu vào, tức là tổng của mỗi đầu vào nhân với trọng số tương ứng của nó.
- Hàm Kích Hoạt (Activation Function): Tổng trọng số sau đó được đưa qua một hàm kích hoạt, thường là một hàm bước, để quyết định đầu ra của Perceptron. Nếu tổng trọng số vượt qua một ngưỡng nhất định, Perceptron sẽ “kích hoạt” và đưa ra đầu ra là 1; ngược lại, nó sẽ không kích hoạt và đưa ra đầu ra là 0.
Perceptron thường được sử dụng trong các tác vụ phân loại đơn giản, nơi nó cố gắng phân tách dữ liệu thành hai lớp. Ví dụ, nó có thể được sử dụng để phân biệt giữa email thường và spam, hoặc để phân loại hình ảnh là chứa một đối tượng cụ thể hay không.
Single Layer Perceptron So với Multi-layer Perceptron
Mặc dù cùng chia sẻ tên gọi “Perceptron”, Single Layer Perceptron và Multi-layer Perceptron (MLP) có những điểm khác biệt đáng kể:
- Số Lớp (Layers):
- Single Layer Perceptron: Chỉ có một lớp duy nhất thực hiện cả việc xử lý đầu vào và đưa ra đầu ra.
- Multi-layer Perceptron: Có nhiều lớp, bao gồm các lớp ẩn (hidden layers) giữa lớp đầu vào và lớp đầu ra. Các lớp ẩn này cho phép MLP xử lý thông tin một cách phức tạp hơn.
- Khả Năng Giải Quyết Vấn Đề:
- Single Layer Perceptron: Thường chỉ phù hợp cho các bài toán phân loại tuyến tính đơn giản.
- Multi-layer Perceptron: Có khả năng giải quyết các bài toán phức tạp hơn, bao gồm cả phân loại phi tuyến.
- Hàm Kích Hoạt:
- Trong khi Single Layer Perceptron thường sử dụng hàm kích hoạt đơn giản như hàm bước, MLP có thể sử dụng nhiều loại hàm kích hoạt phức tạp hơn, như ReLU hoặc Sigmoid, trong các lớp ẩn của nó.
Nhìn chung, Single Layer Perceptron phù hợp cho việc giảng dạy và hiểu biết cơ bản về mạng nơ-ron nhân tạo, trong khi Multi-layer Perceptron thích hợp cho việc giải quyết các vấn đề thực tế phức tạp hơn trong học sâu.
Perceptron bao gồm 4 phần
Input value hoặc One input layer: Lớp đầu vào của perceptron được tạo ra từ các nơ-ron đầu vào nhân tạo và đưa dữ liệu ban đầu vào hệ thống để xử lý thêm.
Weights và Bias:
Weights : Nó thể hiện kích thước hoặc độ bền của kết nối giữa các đơn vị. Nếu trọng số từ nút 1 đến nút 2 có số lượng lớn hơn, thì nơron 1 có ảnh hưởng đáng kể hơn đến nơron.
Bias: Nó giống như số chặn được thêm vào trong một phương trình tuyến tính. Nó là một tham số bổ sung có nhiệm vụ sửa đổi đầu ra cùng với tổng trọng số của đầu vào cho nơ-ron khác.
Net sum: Nó tính tổng tổng.
Activation Function: Một neuron có thể được kích hoạt hay không, được xác định bởi một chức năng kích hoạt. Hàm kích hoạt tính tổng có trọng số và thêm độ lệch với nó để đưa ra kết quả.
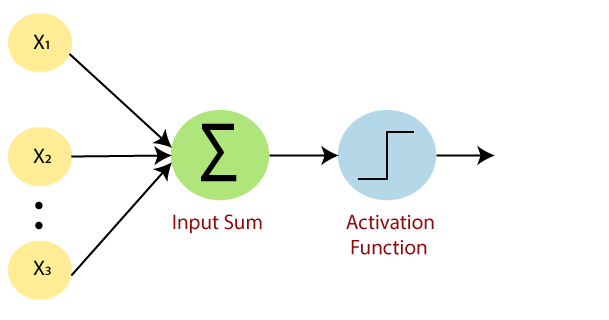
Một mạng nơ-ron tiêu chuẩn trông giống như sơ đồ dưới đây.
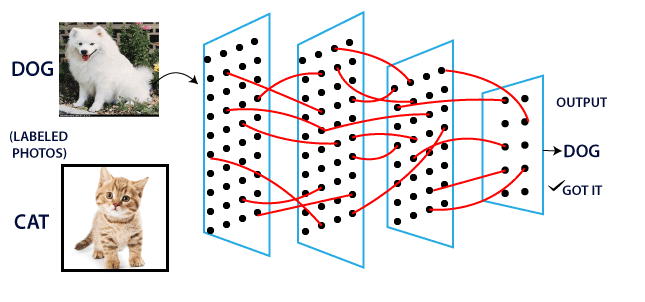
Xây Dựng Single Layer Perceptron với TensorFlow
Hướng Dẫn Từng Bước
- Thiết Lập Môi Trường:
- Đầu tiên, cần cài đặt TensorFlow và các thư viện liên quan. Điều này có thể được thực hiện thông qua pip trong Python.
- Khởi Tạo Mô Hình:
- Sử dụng Keras API trong TensorFlow, bắt đầu bằng việc tạo một mô hình Sequential. Đây là một cách tiện lợi để xây dựng các mô hình layer-by-layer.
- Thêm Lớp Perceptron:
- Thêm một lớp Dense vào mô hình. Lớp Dense là một lớp fully connected, nghĩa là mỗi nơ-ron trong lớp này được kết nối với tất cả nơ-ron ở lớp trước nó. Trong trường hợp của Single Layer Perceptron, lớp này sẽ là lớp duy nhất ngoại trừ lớp đầu vào.
- Cấu Hình Quá Trình Huấn Luyện:
- Chọn một optimizer (ví dụ: SGD hay Adam) và hàm loss (ví dụ: binary_crossentropy cho phân loại nhị phân). Các thông số này sẽ được sử dụng trong quá trình huấn luyện mô hình.
Ví Dụ:
Dưới đây là một ví dụ về cách xây dựng một Single Layer Perceptron trong TensorFlow:
import tensorflow as tf # Xác định mô hình Sequential model = tf.keras.models.Sequential() # Thêm lớp Dense với 1 nơ-ron (đối với bài toán phân loại nhị phân) # Sử dụng hàm kích hoạt sigmoid để đầu ra là một xác suất model.add(tf.keras.layers.Dense(1, input_dim=num_input_features, activation='sigmoid')) # Biên dịch mô hình với optimizer và hàm loss model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
Trong đoạn mã trên, num_input_features là số lượng đặc trưng đầu vào của dữ liệu. Lớp Dense được thiết lập với 1 nơ-ron và hàm kích hoạt sigmoid, phù hợp cho bài toán phân loại nhị phân.
Giới Thiệu về Các Hàm và Lớp trong TensorFlow
- Sequential Model: Là một dạng mô hình đơn giản trong Keras, cho phép tạo các mô hình layer-by-layer một cách tuần tự.
- Dense Layer: Là lớp cơ bản nhất trong mạng nơ-ron, nơi mỗi nơ-ron nhận đầu vào từ tất cả nơ-ron của lớp trước đó.
- Activation Function: Sigmoid được sử dụng ở đây như một hàm kích hoạt để chuyển đổi tổng trọng số thành xác suất.
- Compile Method: Đây là bước cần thiết để cấu hình quá trình học của mô hình, bao gồm việc thiết lập optimizer, hàm loss và các metrics đánh giá.
Thông qua việc sử dụng TensorFlow và Keras API, việc xây dựng và huấn luyện Single Layer Perceptron trở nên đơn giản và trực quan, mở rộng khả năng tiếp cận của học máy đến với nhiều người hơn.
Làm thế nào nó hoạt động?
Perceptron hoạt động theo các bước đơn giản sau:
- Trong bước đầu tiên, tất cả các đầu vào x được nhân với trọng số của chúng là w.
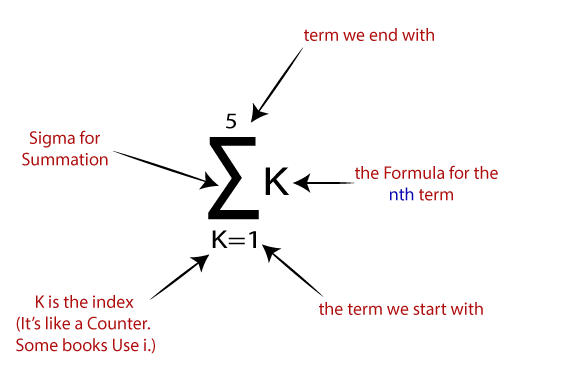
- Trong bước này, hãy thêm tất cả các giá trị tăng lên và gọi chúng là Tổng có trọng số.
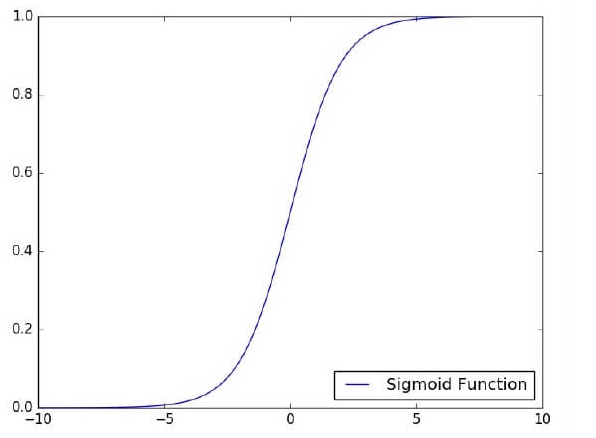
- Trong bước cuối cùng của chúng tôi, hãy áp dụng tổng có trọng số cho một Hàm kích hoạt chính xác.
Ví dụ:
Chức năng kích hoạt bước đơn vị

Có hai kiểu kiến trúc. Các loại này tập trung vào chức năng của mạng nơ-ron nhân tạo như sau:
- Single Layer Perceptron
- Multi-Layer Perceptron
Single Layer Perceptron là mô hình mạng nơ-ron đầu tiên, được đề xuất vào năm 1958 bởi Frank Rosenbluth. Nó là một trong những mô hình sớm nhất cho việc học tập. Mục tiêu của chúng tôi là tìm một hàm quyết định tuyến tính được đo bằng vectơ trọng số w và tham số thiên vị b.
Để hiểu lớp perceptron, cần phải hiểu các mạng nơ-ron nhân tạo (ANN).
Mạng nơ-ron nhân tạo (ANN) là một hệ thống xử lý thông tin, có cơ chế được lấy cảm hứng từ chức năng của các mạch thần kinh sinh học. Một mạng nơ-ron nhân tạo bao gồm một số đơn vị xử lý được kết nối với nhau.
Đây là đề xuất đầu tiên khi mô hình nơ-ron được xây dựng. Nội dung của bộ nhớ cục bộ của nơ-ron chứa một vectơ trọng lượng.
Perceptron vectơ đơn được tính bằng cách tính tổng của vectơ đầu vào nhân với phần tử tương ứng của vectơ, với mỗi lần tăng lượng thành phần tương ứng của vectơ theo trọng số. Giá trị được hiển thị trong đầu ra là đầu vào của một chức năng kích hoạt.
Chúng ta hãy tập trung vào việc triển khai Single Layer Perceptron cho vấn đề phân loại hình ảnh bằng cách sử dụng TensorFlow. Ví dụ tốt nhất về việc vẽ Single Layer Perceptron là thông qua biểu diễn của “hồi quy logistic”.
Bây giờ, Chúng ta phải thực hiện các bước cần thiết sau để đào tạo hồi quy logistic-
Các trọng số được khởi tạo với các giá trị ngẫu nhiên tại nơi bắt đầu của mỗi lần huấn luyện.
Đối với mỗi phần tử của tập huấn luyện, sai số được tính toán với sự khác biệt giữa đầu ra mong muốn và đầu ra thực tế. Sai số tính toán được dùng để điều chỉnh trọng lượng.
Quá trình được lặp lại cho đến khi lỗi thực hiện trên toàn bộ tập huấn luyện nhỏ hơn giới hạn quy định cho đến khi đạt đến số lần lặp tối đa.
Mã hoàn chỉnh của Perceptron lớp đơn
# Import the MINST dataset
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_ ("/tmp/data/", one_hot=True)
import tensorflow as tf
import matplotlib.pyplot as plt
# Parameters
learning_rate = 0.01
training_epochs = 25
batch_size = 100
display_step = 1
# tf Graph Input
x = tf.placeholder("float", [none, 784]) # MNIST data image of shape 28*28 = 784
y = tf.placeholder("float", [none, 10]) # 0-9 digits recognition => 10 classes
# Create model
# Set model weights
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
# Constructing the model
activation=tf.nn.softmaxx(tf.matmul (x, W)+b) # Softmax
of function
# Minimizing error using cross entropy
cross_entropy = y*tf.log(activation)
cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy, reduction_indice = 1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
#Plot settings
avg_set = []
epoch_set = []
# Initializing the variables where init = tf.initialize_all_variables()
# Launching the graph
with tf.Session() as sess:
sess.run(init)
# Training of the cycle in the dataset
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_example/batch_size)
# Creating loops at all the batches in the code
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# Fitting the training by the batch data sess.run(optimizr, feed_dict = {
x: batch_xs, y: batch_ys})
# Compute all the average of loss avg_cost += sess.run(cost, \ feed_dict = {
x: batch_xs, \ y: batch_ys}) //total batch
# Display the logs at each epoch steps
if epoch % display_step==0:
print("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format (avg_cost))
avg_set.append(avg_cost) epoch_set.append(epoch+1)
print ("Training phase finished")
plt.plot(epoch_set,avg_set, 'o', label = 'Logistics Regression Training')
plt.ylabel('cost')
plt.xlabel('epoch')
plt.legend()
plt.show()
# Test the model
correct_prediction = tf.equal (tf.argmax (activation, 1),tf.argmax(y,1))
# Calculating the accuracy of dataset
accuracy = tf.reduce_mean(tf.cast (correct_prediction, "float")) print
("Model accuracy:", accuracy.eval({x:mnist.test.images, y: mnist.test.labels})) Đầu ra của Mã:

Hồi quy logistic được coi là phân tích dự báo. Hồi quy logistic chủ yếu được sử dụng để mô tả dữ liệu và sử dụng để giải thích mối quan hệ giữa biến nhị phân phụ thuộc và một hoặc nhiều biến danh nghĩa hoặc độc lập.


