Bayesian Belief Networks (BBN), còn được gọi là Bayes Networks, Probabilistic Graphical Models, hay Belief Networks, là một loại mô hình đồ thị xác suất. Chúng được sử dụng để biểu diễn và suy luận về các mối quan hệ nguyên nhân giữa một tập hợp các biến ngẫu nhiên. Mỗi nút trong đồ thị đại diện cho một biến ngẫu nhiên, trong khi các cạnh đại diện cho các quan hệ phụ thuộc nguyên nhân giữa các biến đó. Bảng xác suất có điều kiện (CPT) kèm theo mỗi nút cung cấp một cơ sở xác suất để suy luận và đưa ra quyết định.
Lịch sử phát triển của BBN có thể được truy tìm về giữa thế kỷ 20, khi các nhà khoa học bắt đầu áp dụng lý thuyết xác suất vào việc mô hình hóa tri thức và suy luận trong AI. Tuy nhiên, không phải cho đến những năm 1980 và đầu những năm 1990, khi máy tính trở nên mạnh mẽ hơn và các thuật toán mới được phát triển, BBN mới thực sự bùng nổ về mức độ phổ biến và ứng dụng.
Vai trò của BBN trong trí tuệ nhân tạo rất lớn, nhờ khả năng mô hình hóa tri thức phức tạp và thực hiện suy luận dựa trên tri thức đó một cách linh hoạt và mạnh mẽ. BBN cho phép các nhà khoa học máy tính và kỹ sư AI mô hình hóa các quan hệ nguyên nhân giữa các biến trong một cách thức có thể quantize được, từ đó giúp giải quyết các vấn đề từ chẩn đoán y tế đến dự báo thời tiết, từ hệ thống khuyến nghị đến xử lý ngôn ngữ tự nhiên, và nhiều ứng dụng khác. Sự linh hoạt và mạnh mẽ của BBN, kết hợp với khả năng học từ dữ liệu, đã làm cho chúng trở thành một công cụ không thể thiếu trong bộ công cụ của AI hiện đại.
Nguyên lý cơ bản của Bayesian Belief Networks (BBN)
Bayesian Belief Networks (BBN), hay Mạng Bayes, dựa trên lý thuyết xác suất Bayes – một nguyên lý cơ bản trong thống kê và trí tuệ nhân tạo giúp chúng ta suy luận về sự không chắc chắn. Theo lý thuyết này, xác suất của một sự kiện có thể được cập nhật hoặc điều chỉnh dựa trên thông tin mới. Cụ thể, quy tắc Bayes cho phép chúng ta tính xác suất hậu nghiệm (xác suất của một giả thuyết sau khi xem xét bằng chứng) dựa trên xác suất tiền nghiệm (xác suất trước khi xem xét bằng chứng) và khả năng của bằng chứng nếu giả thuyết là đúng.
Cấu trúc của một mạng Bayes bao gồm hai thành phần chính:
Nút
Mỗi nút trong mạng đại diện cho một biến ngẫu nhiên, có thể là một sự kiện, một thuộc tính, hoặc một khái niệm. Nút có thể có giá trị rời rạc hoặc liên tục và thể hiện một phần của tri thức mà mạng được thiết kế để mô hình hóa.
Cạnh
Các cạnh trong mạng biểu diễn quan hệ phụ thuộc giữa các biến. Một cạnh từ nút A đến nút B cho thấy rằng A có ảnh hưởng đến B, hay B phụ thuộc vào A. Cạnh có hướng phản ánh mối quan hệ nguyên nhân giữa các biến và là cơ sở cho quá trình suy luận trong mạng.
Bảng Xác Suất Có Điều Kiện (CPT)
Kèm theo mỗi nút là một Bảng Xác Suất Có Điều Kiện, mô tả xác suất của nút đó dưới các điều kiện hoặc giả định khác nhau về trạng thái của các nút cha (nút đầu vào). CPT là phần then chốt cho phép mạng Bayes thực hiện suy luận xác suất, cung cấp cơ sở để tính toán xác suất của một biến dựa trên trạng thái của các biến khác.
Sự kết hợp của các nút, cạnh, và CPT trong một mạng Bayes cho phép chúng ta mô hình hóa các mối quan hệ phức tạp và thực hiện suy luận xác suất trong một loạt các tình huống đầy thách thức và không chắc chắn. Điều này làm cho BBN trở thành một công cụ mạnh mẽ trong việc mô hình hóa tri thức và quyết định dựa trên tri thức trong trí tuệ nhân tạo.
Biểu đồ mạng Bayes được tạo thành từ các nút và Cung (liên kết có hướng), trong đó:
- Mỗi nút tương ứng với các biến ngẫu nhiên và một biến có thể liên tục hoặc rời rạc.
- Vòng cung hoặc các mũi tên có hướng thể hiện mối quan hệ nhân quả hoặc xác suất có điều kiện giữa các biến ngẫu nhiên. Các liên kết hoặc mũi tên có hướng này kết nối cặp nút trong biểu đồ.
- Các liên kết này thể hiện rằng một nút ảnh hưởng trực tiếp đến nút kia và nếu không có liên kết định hướng có nghĩa là các nút độc lập với nhau
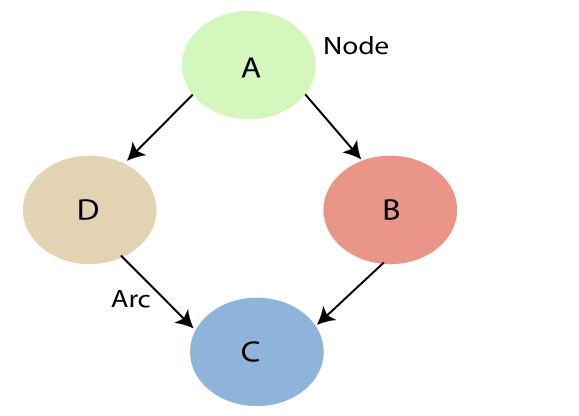
- Trong sơ đồ trên, A, B, C và D là các biến ngẫu nhiên được biểu diễn bởi các nút của biểu đồ mạng.
- Nếu chúng ta đang xem xét nút B, được kết nối với nút A bằng một mũi tên có hướng, thì nút A được gọi là nút cha của nút B.
- Nút C độc lập với nút A.
Lưu ý: Đồ thị mạng Bayes không chứa bất kỳ đồ thị tuần hoàn nào. Do đó, nó được gọi là đồ thị xoay chiều có hướng hoặc DAG.
Suy luận trong Bayesian Belief Networks (BBN)
Trong Bayesian Belief Networks (BBN), suy luận xác suất là quá trình tính toán xác suất của một hoặc nhiều biến ngẫu nhiên khi biết một hoặc nhiều biến khác. Quá trình này dựa trên cấu trúc của mạng và các bảng xác suất có điều kiện (CPT) liên quan đến mỗi nút. Suy luận trong BBN cho phép chúng ta đưa ra các quyết định hoặc dự đoán dựa trên tri thức không đầy đủ hoặc không chắc chắn.
Cách Thức Suy Luận Xác Suất Trong BBN
Suy luận trong BBN thường được thực hiện thông qua hai phương pháp chính: suy luận tiến (forward chaining) và suy luận ngược (backward chaining).
- Suy Luận Tiến: Bắt đầu từ biến nguyên nhân và suy ra xác suất của các biến kết quả. Ví dụ, biết xác suất của các điều kiện bệnh và suy luận về triệu chứng có thể xuất hiện.
- Suy Luận Ngược: Bắt đầu từ biến kết quả hoặc triệu chứng và suy ngược lại tìm xác suất của các nguyên nhân có thể. Ví dụ, biết triệu chứng và suy luận về xác suất của các bệnh có thể gây ra triệu chứng đó.
Suy luận trong BBN sử dụng quy tắc Bayes để cập nhật xác suất dựa trên thông tin mới, cho phép mô hình đưa ra suy luận dựa trên tri thức và bằng chứng có sẵn.
Ví Dụ Minh Họa Suy Luận Xác Suất
Giả sử chúng ta có một BBN với ba nút: “Viêm Họng” (A), “Sốt” (B), và “Ho” (C), nơi “Viêm Họng” gây ra “Sốt” và “Ho”. Biết rằng một bệnh nhân đang ho (C=true), chúng ta muốn suy luận về xác suất bệnh nhân đó bị “Viêm Họng” (A).
Sử dụng BBN và các CPT liên quan, chúng ta có thể tính toán xác suất có điều kiện của “Viêm Họng” dựa trên “Ho” như sau:
- Xem xét CPT liên quan đến “Ho” và mối quan hệ của nó với “Viêm Họng”.
- Áp dụng quy tắc Bayes để cập nhật xác suất của “Viêm Họng” dựa trên thông tin “Ho”.
Giả sử, sau khi áp dụng suy luận, chúng ta thu được xác suất cao của “Viêm Họng” dựa trên việc bệnh nhân có triệu chứng ho. Kết quả này giúp chúng ta đưa ra quyết định chẩn đoán hoặc khuyến nghị điều trị phù hợp.
Qua ví dụ trên, suy luận trong BBN cho phép chúng ta đưa ra các quyết định dựa trên tri thức và bằng chứng có sẵn, dù trong tình huống không chắc chắn. Điều này làm cho BBN trở thành công cụ quý giá trong việc mô hình hóa và suy luận trong nhiều lĩnh vực của trí tuệ nhân tạo.
Học Máy và BBN
Trong lĩnh vực học máy, Bayesian Belief Networks (BBN) đóng một vai trò quan trọng bằng cách cung cấp một phương pháp để học từ dữ liệu và đồng thời xử lý sự không chắc chắn. BBN kết hợp lý thuyết xác suất Bayes với kiến thức chuyên môn về mối quan hệ nguyên nhân giữa các biến, cho phép mô hình hóa tri thức dưới dạng đồ thị có hướng và xác suất.
Cách BBN Được Sử Dụng Để Học Từ Dữ Liệu
Học từ dữ liệu trong BBN thường diễn ra theo hai hướng: học cấu trúc và học tham số.
- Học Cấu Trúc: Quá trình này bao gồm việc xác định cấu trúc của mạng, tức là các nút và cạnh (mối quan hệ) giữa chúng, dựa trên dữ liệu. Các thuật toán học cấu trúc tìm kiếm qua không gian các cấu trúc mạng khả dĩ để tìm ra cấu trúc phản ánh mối quan hệ nguyên nhân giữa các biến một cách chính xác nhất.
- Học Tham Số: Sau khi cấu trúc mạng được xác định, học tham số tập trung vào việc ước lượng các bảng xác suất có điều kiện (CPT) cho mỗi nút. Việc này thường dựa vào dữ liệu để ước lượng xác suất của mỗi nút dựa vào trạng thái của các nút cha.
Ưu Điểm của Việc Sử Dụng BBN Trong Việc Mô Hình Hóa Dữ Liệu Phức Tạp và Không Chắc Chắn
- Xử Lý Sự Không Chắc Chắn: BBN là công cụ mạnh mẽ trong việc mô hình hóa và xử lý sự không chắc chắn, cho phép suy luận dựa trên thông tin không đầy đủ hoặc có nhiễu.
- Khả Năng Diễn Giải: So với các mô hình học sâu, BBN cung cấp khả năng diễn giải cao về mối quan hệ nguyên nhân giữa các biến, giúp người dùng dễ dàng hiểu và kiểm tra mô hình.
- Tích Hợp Tri Thức Chuyên Môn: BBN cho phép tích hợp tri thức chuyên môn dưới dạng mối quan hệ nguyên nhân giữa các biến, cải thiện khả năng mô hình hóa dựa trên kiến thức đã có.
- Đa Dạng Ứng Dụng: BBN có thể được áp dụng trong nhiều lĩnh vực khác nhau, từ chẩn đoán y tế, dự báo thời tiết, đến quản lý rủi ro tài chính, chứng minh tính linh hoạt và mạnh mẽ của mô hình.
BBN kết hợp tri thức chuyên môn với dữ liệu, cung cấp một phương pháp mạnh mẽ và linh hoạt để học và suy luận trong môi trường phức tạp và không chắc chắn. Sự tích hợp giữa lý thuyết xác suất và học máy mở ra cơ hội lớn hơn
Ứng dụng của Bayesian Belief Networks (BBN)
Bayesian Belief Networks (BBN) đã tìm thấy ứng dụng trong một loạt các lĩnh vực trong trí tuệ nhân tạo, cung cấp giải pháp cho các vấn đề phức tạp thông qua suy luận xác suất và mô hình hóa tri thức. Dưới đây là một số ứng dụng thực tế của BBN trong AI:
Chẩn Đoán Y Khoa
Trong y khoa, BBN được sử dụng để chẩn đoán các bệnh dựa trên một tập hợp các triệu chứng và dấu hiệu bệnh lý. Ví dụ, một mạng Bayes có thể mô hình hóa mối quan hệ nguyên nhân giữa các triệu chứng và các tình trạng bệnh khác nhau, cho phép bác sĩ đưa ra chẩn đoán chính xác hơn dựa trên thông tin sẵn có. Một ví dụ cụ thể là mô hình DIAGNOSER dùng để chẩn đoán bệnh tim mạch.
Dự Báo Thời Tiết
BBN cũng được áp dụng trong dự báo thời tiết, nơi chúng giúp dự đoán các sự kiện thời tiết dựa trên một loạt các biến đầu vào, từ dữ liệu vệ tinh đến các quan sát mặt đất. Sự phức tạp và sự không chắc chắn của các mô hình thời tiết được xử lý hiệu quả thông qua mô hình hóa BBN.
Hệ Thống Khuyến Nghị
Trong lĩnh vực thương mại điện tử và dịch vụ trực tuyến, BBN được sử dụng để phát triển hệ thống khuyến nghị cá nhân hóa. Bằng cách mô hình hóa sở thích của người dùng và hành vi mua hàng, mạng Bayes có thể dự đoán và đề xuất sản phẩm hoặc dịch vụ phù hợp với từng người dùng. Một ứng dụng cụ thể là hệ thống khuyến nghị phim trên các nền tảng streaming.
Phát Hiện Gian Lận
Trong ngành tài chính và ngân hàng, BBN được ứng dụng để phát hiện gian lận bằng cách suy luận các mẫu hành vi bất thường từ dữ liệu giao dịch. Các mô hình có thể phát hiện các giao dịch đáng ngờ và cảnh báo cho ngân hàng hoặc người dùng, giảm thiểu rủi ro tài chính.
Quản Lý Rủi Ro và Hỗ Trợ Quyết Định
BBN cung cấp công cụ mạnh mẽ cho việc quản lý rủi ro và hỗ trợ quyết định trong nhiều lĩnh vực từ quản lý dự án đến chính sách công. Mạng Bayes giúp đánh giá rủi ro và lợi ích của các quyết định khác nhau dựa trên dữ liệu và kiến thức chuyên môn.
Các ví dụ này minh họa cho sự đa dạng và tính linh hoạt của BBN trong việc giải quyết các vấn đề thực tế. Sự kết hợp giữa mô hình hóa tri thức, suy luận xác suất và học từ dữ liệu giúp BBN trở thành một công cụ quý giá trong tay các nhà nghiên cứu và nhà phát triển AI
Giải thích về mạng Bayes
Hãy hiểu về mạng Bayes qua một ví dụ bằng cách tạo một biểu đồ xoay chiều có hướng:
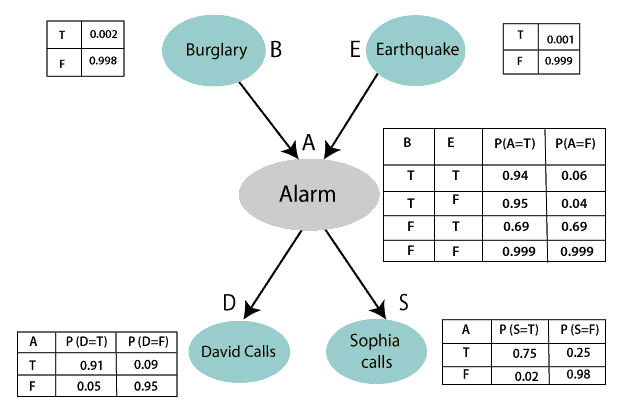
Ví dụ: Harry đã lắp đặt một thiết bị báo Burglary mới tại nhà của mình để phát hiện Burglary. Báo động phản hồi một cách đáng tin cậy khi phát hiện một vụ Burglary nhưng cũng phản ứng với các trận earthquake nhỏ. Harry có hai người hàng xóm là David và Sophia, những người đã nhận trách nhiệm thông báo cho Harry tại nơi làm việc khi họ nghe thấy tiếng chuông báo động. David luôn gọi điện cho Harry khi nghe thấy tiếng chuông báo thức, nhưng đôi khi anh ấy cảm thấy bối rối với tiếng chuông điện thoại và các cuộc gọi cũng vào thời điểm đó. Mặt khác, Sophia thích nghe nhạc cao nên đôi khi lỡ nghe chuông báo thức. Ở đây chúng tôi muốn tính xác suất của Báo động Burglary.
Vấn đề:
Tính xác suất để chuông báo động vang lên, nhưng không có một vụ Burglary hay một trận earthquake nào xảy ra, và David và Sophia đều gọi cho Harry.
Giải pháp:
- Mạng Bayes cho vấn đề trên được đưa ra dưới đây. Cấu trúc mạng cho thấy Burglary và earthquake là nút chính của báo động và ảnh hưởng trực tiếp đến xác suất báo động phát ra, nhưng các cuộc gọi của David và Sophia phụ thuộc vào xác suất báo động.
- Mạng lưới đại diện rằng giả định của chúng tôi không trực tiếp cảm nhận được vụ Burglary và cũng không nhận thấy trận earthquake nhỏ, và họ cũng không quy trước khi gọi điện.
- Các phân phối có điều kiện cho mỗi nút được đưa ra dưới dạng bảng xác suất có điều kiện hoặc CPT.
- Mỗi hàng trong CPT phải có tổng bằng 1 vì tất cả các mục trong bảng đại diện cho một tập hợp đầy đủ các trường hợp cho biến.
- Trong CPT, một biến boolean có k boolean cha chứa 2K xác suất. Do đó, nếu có hai parent, thì CPT sẽ chứa 4 giá trị xác suất
Danh sách tất cả các sự kiện xảy ra trong mạng này:
- Burglary (B)
- Earthquake(E)
- Alarm(A)
- David Calls(D)
- Sophia calls(S)
Chúng ta có thể viết các sự kiện của trạng thái vấn đề
nt dưới dạng xác suất: P [D, S, A, B, E], có thể viết lại câu xác suất ở trên bằng cách sử dụng phân phối xác suất chung:
P [D, S, A, B, E] = P [D | S, A, B, E]. P [S, A, B, E]
= P [D | S, A, B, E]. P [S | A, B, E]. P [A, B, E]
= P [D | A]. P [S | A, B, E]. P [A, B, E]
= P [D | A]. P [S | A]. P [A | LÀ]. P [B, E]
= P [D | A ]. P [S | A]. P [A | LÀ]. P [B | E]. P [E]
Hãy lấy xác suất quan sát được cho thành phần Burglary và earthquake:
- P (B = True) = 0,002, là xác suất xảy ra Burglary.
- P (B = Sai) = 0,998, là xác suất để không có Burglary.
- P (E = True) = 0,001, là xác suất của một trận earthquake nhỏ
- P (E = False) = 0,999, là xác suất để không xảy ra earthquake.
Chúng tôi có thể cung cấp các xác suất có điều kiện theo bảng dưới đây:
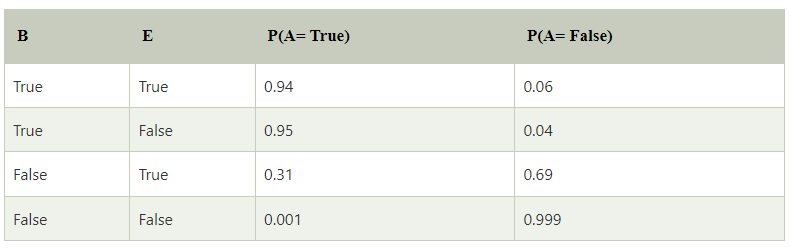
Bảng xác suất có điều kiện cho Báo động A:
Xác suất có điều kiện của Báo động A phụ thuộc vào Burglary và earthquake:
Bảng xác suất có điều kiện cho David Calls:
Xác suất có điều kiện của David mà anh ta sẽ gọi phụ thuộc vào xác suất của Báo động.

Bảng xác suất có điều kiện cho Sophia Calls:
Xác suất có điều kiện của Sophia mà cô ấy gọi là tùy thuộc vào Nút mẹ của nó là “Báo động”.

Từ công thức phân phối chung, chúng ta có thể viết bài toán dưới dạng phân phối xác suất:
P (S, D, A, ¬B, ¬E) = P (S | A) * P (D | A) * P (A | ¬B ^ ¬E) * P (¬B) * P (¬E ).
= 0,75 * 0,91 * 0,001 * 0,998 * 0,999
= 0,00068045.
Do đó, mạng Bayes có thể trả lời bất kỳ truy vấn nào về miền bằng cách sử dụng Phân phối chung.
Ngữ nghĩa của Mạng Bayes: