Trong toán học và khoa học máy tính, đồ thị là một cấu trúc dữ liệu quan trọng, được định nghĩa là một tập hợp các đỉnh (hoặc nút) được kết nối bởi các cạnh. Mỗi cạnh có thể biểu diễn một mối quan hệ hoặc một kết nối giữa hai đỉnh, tạo ra một mô hình mạng lưới phức tạp có khả năng biểu diễn nhiều loại mối quan hệ và cấu trúc trong thế giới thực. Đồ thị có thể được phân loại thành nhiều loại khác nhau, bao gồm đồ thị có hướng và vô hướng, đồ thị trọng số và không trọng số, tùy thuộc vào tính chất của các cạnh và đỉnh.
Tầm quan trọng của đồ thị trong các lĩnh vực toán học và khoa học máy tính là không thể phủ nhận. Đồ thị cung cấp một công cụ mạnh mẽ để mô hình hóa và giải quyết các vấn đề phức tạp, từ lý thuyết đồ thị, tối ưu hóa mạng, phân tích mạng xã hội, cho đến thiết kế mạng máy tính và mạng giao thông. Lịch sử phát triển của đồ thị bắt đầu từ thế kỷ 18 với bài toán nổi tiếng của Euler về “Bảy cây cầu của Königsberg”, đánh dấu sự khởi đầu của lý thuyết đồ thị như một ngành toán học riêng biệt. Kể từ đó, lý thuyết đồ thị và ứng dụng của nó đã phát triển mạnh mẽ và trở thành một phần không thể thiếu trong nghiên cứu và phát triển công nghệ, giúp giải quyết nhiều vấn đề từ lý thuyết đến thực tiễn.
Định nghĩa về Đồ thị
Đồ thị G bao gồm hai thứ:
1. Một tập hợp V = V (G) có các phần tử được gọi là đỉnh, điểm hay nút của G.
2. Tập hợp E = E (G) gồm một cặp đỉnh phân biệt không có thứ tự được gọi là các cạnh của G.
3. Chúng ta biểu thị một đồ thị như vậy bởi G (V, E) các đỉnh u và v được cho là kề nhau nếu có một cạnh e = {u, v}.
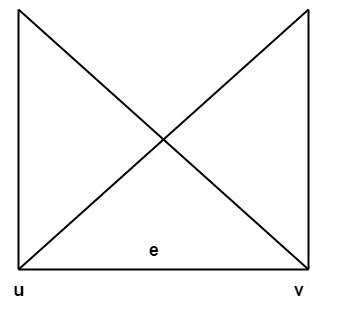
4. Trong trường hợp như vậy u và v được gọi là điểm cuối của e = {u, v} và e được cho là nối u và v.
Cấu trúc cơ bản về đồ thị
Cấu trúc cơ bản của đồ thị bao gồm hai thành phần chính: đỉnh (vertices) và cạnh (edges). Đỉnh thường biểu diễn các đối tượng, trong khi cạnh kết nối các đỉnh biểu diễn mối quan hệ hay tương tác giữa các đối tượng đó. Trong một đồ thị, cạnh có thể được biểu diễn bằng một đường nối giữa hai đỉnh, và mỗi cạnh có thể kết nối một cặp đỉnh theo một hoặc hai chiều.
Đồ thị có thể được phân loại thành đồ thị có hướng và đồ thị vô hướng tùy thuộc vào tính chất của các cạnh. Trong đồ thị có hướng (directed graphs), mỗi cạnh có một hướng xác định, từ một đỉnh đến một đỉnh khác, biểu diễn mối quan hệ một chiều. Trong khi đó, đồ thị vô hướng (undirected graphs) có các cạnh không hướng, biểu diễn mối quan hệ hai chiều hoặc không xác định hướng, nghĩa là mối quan hệ giữa hai đỉnh là đối xứng.
Ngoài ra, đồ thị còn có thể được phân biệt dựa trên việc có sử dụng trọng số trên các cạnh hay không. Đồ thị trọng số (weighted graphs) có các cạnh được gán một giá trị số hoặc “trọng số”, thường biểu diễn chi phí, khoảng cách, hoặc một đặc tính quan trọng nào đó của mối quan hệ. Trong khi đó, đồ thị không trọng số (unweighted graphs) là đồ thị mà tất cả các cạnh đều có cùng giá trị hoặc không có trọng số cụ thể.
Sự hiểu biết về cấu trúc cơ bản này của đồ thị và sự phân biệt giữa các loại đồ thị khác nhau là rất quan trọng, vì nó cung cấp nền tảng cho việc thiết kế, phân tích và áp dụng các thuật toán đồ thị trong giải quyết nhiều vấn đề phức tạp trong toán học, khoa học máy tính, và nhiều lĩnh vực ứng dụng khác.
Bậc của một đỉnh
Bậc của đỉnh là số cạnh của đỉnh v. Vòng lặp tự được tính hai lần. Bậc của một đỉnh được ký hiệu là d (v).
Ví dụ 1: Hãy xem xét đồ thị G được hiển thị trong hình. Xác định tung độ của mỗi đỉnh.
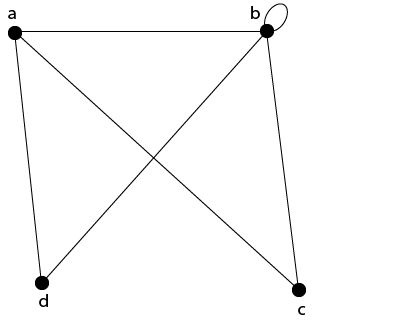
Bài giải: Bậc của mỗi đỉnh như sau:
d (a) = 3; d (b) = 5; d (c) = 2; d (d) = 2.
Ví dụ 2: Xác minh rằng tổng các bậc của tất cả các đỉnh là chẵn đối với đồ thị được hiển thị trong hình:
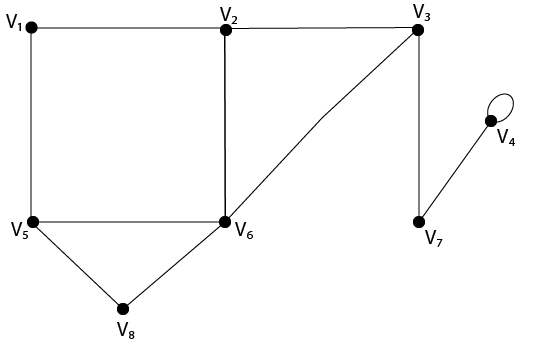
Bài giải: Tổng bậc của tất cả các đỉnh là:
= d (v1) + d (v2) + d (v3) + d (v4) + d (v5) + d (v6) + d (v7) + d (v8)
= 2 + 3 + 3 + 3 + 3 + 4 + 2 + 2 = 22, là số chẵn.
Ví dụ 3: Xác minh rằng có số lượng đỉnh có độ lẻ chẵn trong biểu đồ được hiển thị trong hình:

Bài giải: Số đỉnh có bậc lẻ là 8 và mỗi đỉnh có bậc ba trong đồ thị trên. Do đó, chúng ta có số đỉnh chẵn có bậc lẻ.
Đường đi
Đường đi có độ dài n là một dãy gồm n + 1 đỉnh của đồ thị, trong đó mỗi cặp đỉnh là một cạnh của đồ thị.
Đường dẫn đơn giản: Đường đi được gọi là đường đơn giản nếu không có cạnh nào được lặp lại trong đường đi, tức là tất cả các đỉnh là khác biệt ngoại trừ đỉnh đầu tiên bằng với đỉnh cuối cùng.
Một đường dẫn sơ cấp: Đường đi được gọi là đường sơ cấp nếu không có đỉnh nào được lặp lại trong đường dẫn, tức là tất cả các đỉnh đều khác biệt.
Mạch hoặc Đường đi kín: Đường mạch hoặc đường dẫn kín là một đường dẫn trong đó bắt đầu và kết thúc tại cùng một đỉnh, tức là v0 = vn.
Đường dẫn mạch đơn giản: Mạch điện đơn giản là một đường dẫn đơn giản là một mạch điện.
Ví dụ: Hãy xem xét biểu đồ được hiển thị trong hình: Cho một ví dụ sau:
Một đường dẫn đơn giản từ V1 đến V6.
Một đường dẫn sơ cấp từ V1 đến V6.
Một con đường đơn giản không phải là cơ bản từ V1 đến V6.
Một con đường không đơn giản và bắt đầu từV2.
Một mạch đơn giản bắt đầu từ V1
Một mạch không đơn giản và bắt đầu từ V2.
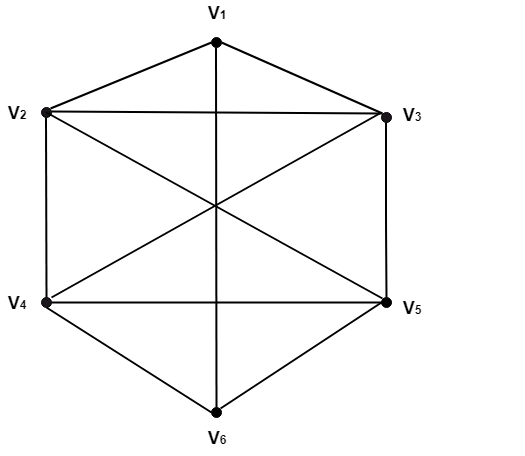
Đáp án:
Một đường dẫn đơn giản từ V1 đến V6.
V1, V2, V3, V4, V5, V6.
Một đường dẫn sơ cấp từ V1 đến V6.
V1, V2, V3, V5, V4, V6.
Một con đường đơn giản không phải là cơ bản từ V1 đến V6.
V1, V2, V3, V5, V2, V4, V6.
Một con đường không đơn giản và bắt đầu từ V2.
V2, V3, V4, V5, V3, V4, V6.
Một đoạn mạch đơn giản bắt đầu từ V1.
V1, V2, V4, V6, V5, V3, V1
Một mạch không đơn giản và bắt đầu từ V2.
V2, V3, V1, V2, V5, V4, V2.
- Đỉnh mặt dây chuyền: Một đỉnh có bậc một được gọi là Đỉnh mặt dây chuyền.
- Cạnh mặt dây chuyền: Cạnh duy nhất nối với đỉnh mặt dây chuyền được gọi là Cạnh mặt dây chuyền.
- Đỉnh lẻ: Một đỉnh có bậc lẻ được gọi là đỉnh lẻ.
- Đỉnh chẵn: Đỉnh có tung độ được gọi là đỉnh chẵn.
- Cạnh kề: Một cạnh được gọi là sự cố với các đỉnh được nối.
- Các đỉnh liền kề: Hai đỉnh được gọi là kề nhau nếu một cạnh liên kết chúng. Nếu có một cạnh (u, v), thì ta có thể nói đỉnh u là kề với đỉnh v, và đỉnh v là kề với đỉnh u.
Ví dụ: Hãy xem xét biểu đồ như trong hình:
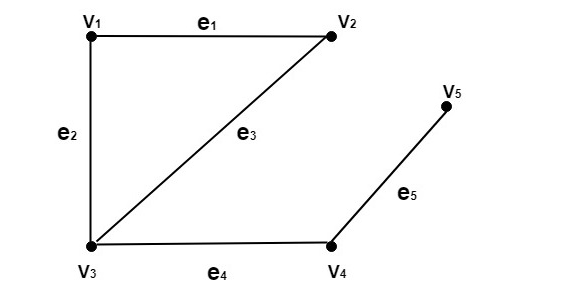
Xác định những điều sau:
- Dọc mặt dây chuyền
- Viền mặt dây chuyền
- Các đỉnh lẻ
- Dọc chẵn
- Cạnh kề
- Dọc liền kề
- Đỉnh V5 là đỉnh mặt dây chuyền.
- Cạnh (V4, V5) hoặc e5 là cạnh mặt dây chuyền.
- Các đỉnh V3 và V5 là các đỉnh lẻ.
- Các đỉnh V1, V2 và V4 là các đỉnh chẵn.
- Cạnh e1 là một sự cố trên V1 và V2.
- Cạnh e2 là một sự cố trên V1 và V3.
- Cạnh e3 là sự cố trên V2 và V3.
- Cạnh e4 là một sự cố trên V3 và V4.
- Cạnh e5 là một sự cố trên V4 và V5.
- Đỉnh V1 tiếp giáp với V2 và V3.
- Đỉnh V2 tiếp giáp với V1 và V2.
- Đỉnh V3 tiếp giáp với V1 và V4
- Đỉnh V4 tiếp giáp với V3 và V5
- Đỉnh V5 kề với V4.
Self-Loop: Một vòng lặp tự là một cạnh e nếu nó có cùng điểm cuối.
Đồ thị trong hình chứa vòng lặp tự tại đỉnh b, tức là, e = (b, b).
Đỉnh cô lập: Một đỉnh có bậc 0 được gọi là đỉnh cô lập.
Tập cắt: Xét một đồ thị G = (V, E). Một tập cắt cho G là tập các cạnh nhỏ nhất sao cho việc loại bỏ tập hợp đó, làm ngắt kết nối đồ thị trong khi việc loại bỏ bất kỳ tập hợp con thích hợp nào của tập hợp này sẽ để lại một đồ thị con được kết nối .
Ví dụ: Hãy xem xét biểu đồ được hiển thị trong hình. Xác định tập hợp cắt cho nhóm này.
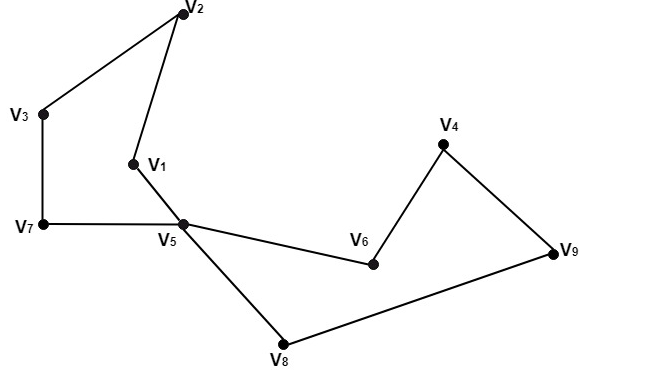
Lời giải: Đối với đồ thị này, tập cạnh {(V1, V5), (V7, V5)} là tập cắt. Sau khi xóa tập hợp, chúng tôi đã để lại với một đồ thị con bị ngắt kết nối. Trong khi sau khi loại bỏ bất kỳ tập hợp con thích hợp nào của nó, chúng tôi đã để lại với một đồ thị con được kết nối.
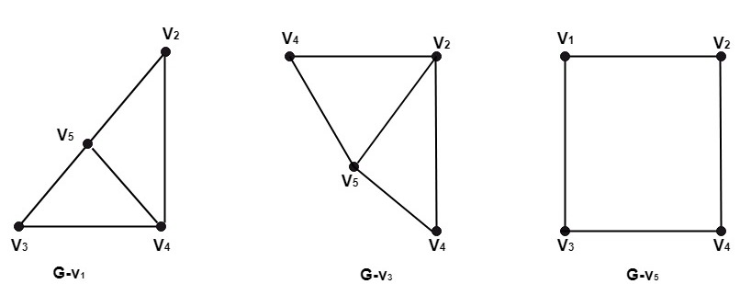
Điểm cắt hoặc đỉnh cắt: Xét đồ thị G = (V, E). Điểm cắt của đồ thị G là đỉnh v sao cho G-v có nhiều thành phần liên thông hơn G hoặc bị ngắt kết nối. Đồ thị con G-v nhận được bằng cách xóa đỉnh v khỏi đồ thị G và cũng xóa toàn bộ sự cố các cạnh trên v.
Ví dụ: Hãy xem xét biểu đồ được hiển thị trong hình. Xác định các đồ thị con
(i) G-v1 (ii) G-v3 (iii) G-v5
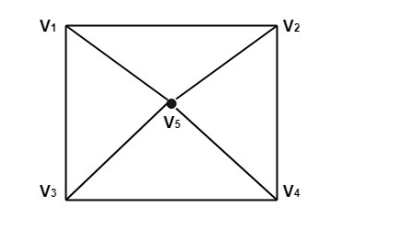
- Biểu đồ con G-v1 được hiển thị trong hình
- Đồ thị con G-v3 được hiển thị trong hình
- Đồ thị con G-v5 được hiển thị trong hình
Cầu (Cut Edges): Xét đồ thị G = (V, E). Một cầu cho đồ thị G, là một cạnh e sao cho G-e có nhiều thành phần liên thông hơn G hoặc ngắt kết nối.
Ví dụ: Hãy xem xét biểu đồ được hiển thị trong hình. Xác định các đồ thị con
(i) G-e1 (ii) G-e3 (iii) G-e4

Biểu đồ con G-e1 được hiển thị trong hình
Biểu đồ con G-e3 được hiển thị trong hình
Biểu đồ con G-e4 được hiển thị trong hình
Biểu diễn đồ thị
Biểu diễn đồ thị là một khía cạnh quan trọng trong việc phân tích và làm việc với đồ thị trong lý thuyết và ứng dụng. Có hai phương pháp chính để biểu diễn đồ thị một cách trừu tượng là sử dụng ma trận kề và danh sách kề.
Ma trận kề là một ma trận vuông (A) với kích thước bằng số lượng đỉnh của đồ thị, trong đó mỗi phần tử (A[i][j]) biểu diễn mối quan hệ giữa đỉnh (i) và (j). Trong trường hợp đồ thị vô hướng, nếu đỉnh (i) và (j) được nối với nhau bởi một cạnh, (A[i][j]) và (A[j][i]) sẽ được đặt là 1 (hoặc trọng số của cạnh nếu là đồ thị trọng số); nếu không, chúng sẽ được đặt là 0. Đối với đồ thị có hướng, chỉ phần tử (A[i][j]) được đặt là 1 nếu có một cạnh từ (i) đến (j). Ma trận kề cung cấp một cách toàn diện để biểu diễn mọi thông tin về mối quan hệ giữa các đỉnh, nhưng nó có thể không hiệu quả về mặt bộ nhớ khi đồ thị thưa.
Danh sách kề là một cách biểu diễn thay thế, nơi mỗi đỉnh của đồ thị được liên kết với một danh sách chứa tất cả các đỉnh mà nó kết nối trực tiếp. Đối với mỗi đỉnh, danh sách kề liệt kê tất cả các đỉnh láng giềng, tạo điều kiện thuận lợi cho việc duyệt và xử lý đồ thị. Đây là một cách biểu diễn hiệu quả hơn đối với đồ thị thưa, nơi số lượng cạnh nhỏ so với số lượng đỉnh.
Bên cạnh cách biểu diễn trừu tượng, biểu diễn đồ thị trực quan cũng rất quan trọng, đặc biệt trong việc phân tích và hiểu đồ thị. Đồ thị có thể được vẽ trên mặt phẳng với các đỉnh được biểu diễn bởi các điểm và các cạnh được biểu diễn bởi các đường nối giữa các điểm này. Biểu diễn trực quan giúp con người dễ dàng nhận biết các mẫu và cấu trúc trong đồ thị, như các nhóm đỉnh, chu trình, hoặc thành phần liên thông, và là công cụ không thể thiếu trong việc giáo dục và trình bày đồ thị.
Tổng hợp lại, việc lựa chọn phương pháp biểu diễn phụ thuộc vào bản chất và kích thước của đồ thị cũng như mục đích sử dụng, với mỗi phương pháp đều có ưu và nhược điểm riêng biệt.


