Rate this post

Tóm tắt nội dung

Cây nhị phân là gì?

Cây nhị phân là một cấu trúc dữ liệu phân cấp trong đó mỗi nút có nhiều nhất hai nút con thường được gọi là nút con trái và nút con phải.

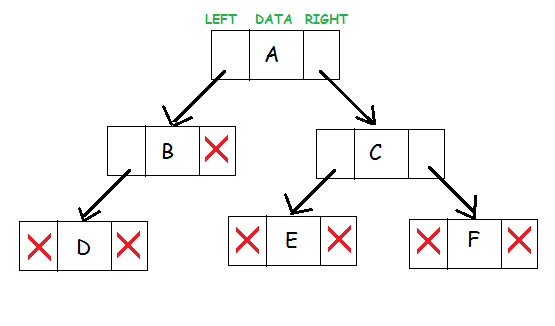
Mỗi nút chứa ba thành phần:

Con trỏ sang cây con bên trái
Con trỏ sang cây con bên phải
Phần tử dữ liệu

Nút trên cùng của cây được gọi là gốc. Một cây trống được biểu diễn bằng con trỏ NULL .

Một đại diện của cây nhị phân được hiển thị:

Các thuật ngữ chung

Gốc: Nút trên cùng của cây.
Cha: Mọi nút (không bao gồm gốc) trong cây được kết nối bằng một cạnh có hướng từ chính xác một nút khác. Nút này được gọi là nút cha.
Con: Một nút kết nối trực tiếp với một nút khác khi di chuyển ra khỏi gốc.
Nút lá / nút ngoài: là node không có node con nào khác.
Nút bên trong: là node có ít nhất 1 node con.
Độ sâu của một node: số cạnh nối từ Root đến node đó.
Chiều cao của một Node: Số cạnh từ node root đến node lá sâu nhất.

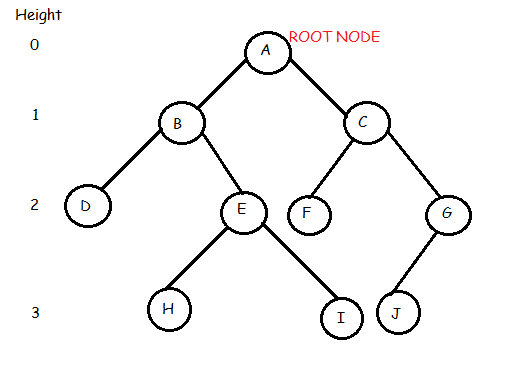
Trong cây nhị phân trên chúng ta thấy rằng nút gốc là Một . Cây có 10 nút với 5 nút nội bộ, tức là A, B, C, E, G và 5 nút bên ngoài, ví dụ, D, F, H, I, J . Chiều cao của cây là 3. B là công ty mẹ của D và E khi D và E là con của B .

Chiều cao của cây nhị phân

Chiều cao của một node trong cây nhị phân là số cạnh lớn nhất trong đường dẫn từ nút lá đến nút đích. Nếu nút đích không có bất kỳ nút nào khác được kết nối với nó, chiều cao của nút đó sẽ là 0.

Chiều cao của cây nhị phân là chiều cao của nút gốc trong toàn bộ cây nhị phân. Nói cách khác, chiều cao của cây nhị phân bằng số cạnh lớn nhất từ gốc đến nút lá xa nhất.

Một khái niệm tương tự trong cây nhị phân là độ sâu của cây. Độ sâu của một node trong cây nhị phân là tổng số cạnh từ nút gốc đến nút đích. Tương tự, độ sâu của cây nhị phân là tổng số cạnh từ nút gốc đến nút lá xa nhất.

Một quan sát quan trọng ở đây là khi chúng tôi tính toán độ sâu của toàn bộ cây nhị phân, nó tương đương với chiều cao của cây nhị phân.

Các bài viết liên quan:

Ưu điểm của cây:

Cây rất hữu ích và được sử dụng thường xuyên, bởi vì chúng có một số ưu điểm rất nghiêm trọng:

Cây phản ánh mối quan hệ cấu trúc trong dữ liệu.
Cây được sử dụng để đại diện cho các thứ bậc.
Cây cung cấp một hiệu quả cho chèn và tìm kiếm.
Cây là dữ liệu rất linh hoạt, cho phép di chuyển các cây con xung quanh với nỗ lực tối thiểu.

Các loại cây nhị phân (Dựa trên cấu trúc)

Cây nhị phân có gốc: Nó có một nút gốc và mỗi nút có ít nhất hai nút con.

Cây nhị phân đầy đủ: Là cây trong đó mỗi nút trong cây có 0 hoặc 2 nút con.

Số nút, n , trong một cây nhị phân đầy đủ ít nhất là n = 2h – 1, và tối đa là n = 2 h + 1 – 1 , trong đó h là chiều cao của cây.
Số nút lá l , trong cây nhị phân đầy đủ là số, L của các nút bên trong + 1, tức là, l = L + 1 .

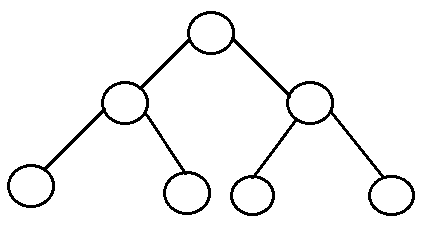
Cây nhị phân hoàn hảo: Là cây nhị phân trong đó tất cả các nút bên trong có hai nút con và tất cả các lá có cùng độ sâu hoặc cùng mức.

Một cây nhị phân hoàn hảo với l lá có n = 2l-1 nút.
Trong cây nhị phân hoàn hảo, l = 2h và n = 2h + 1 – 1 trong đó, n là số nút, h là chiều cao của cây và l là số nút lá

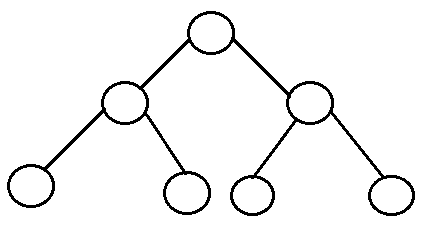
Cây nhị phân hoàn chỉnh: Là cây nhị phân trong đó mọi cấp, ngoại trừ cấp cuối cùng, được lấp đầy hoàn toàn và tất cả các nút ở bên trái càng xa càng tốt.

Số nút bên trong trong một cây nhị phân hoàn chỉnh gồm n nút là tầng (n / 2) .

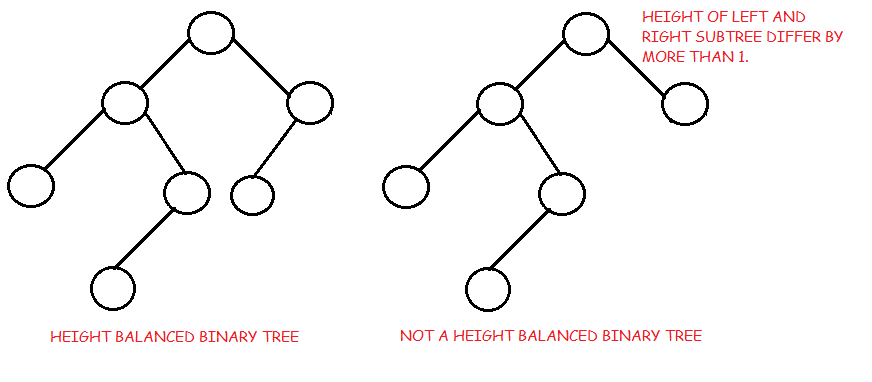
Cây nhị phân cân bằng: Cây nhị phân có chiều cao cân bằng nếu nó thỏa mãn các ràng buộc sau:

Chiều cao của cây phía trái và cây phía bên phải chỉ hơn nhau là 1, VÀ
Cây con bên trái phải được cân bằng, VÀ
Cây con bên phải phải được cân bằng
Một cây trống thường có chiều cao cân đối.
Chiều cao của cây nhị phân cân bằng là O ( Log n ) với n là số nút.

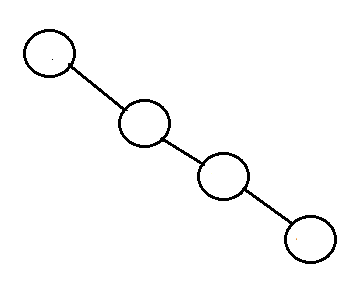
Degenarate tree: Là cây mà mỗi nút cha chỉ có một nút con. Nó hoạt động giống như một danh sách được liên kết.

Cây tìm kiếm nhị phân

Cây nhị phân tìm kiếm là loại cấu trúc dữ liệu có độ phức tạp thuật toán thêm và xóa cây tốt.
Nó bao gồm nhiều node, nơi được lưu trữ dữ liệu và cũng có những liên kết với nhiều nhất hai node con khác. Đó là một mối quan hệ cha con của node và node khác, điều này giúp cây nhị phân tìm kiếm một cấu trúc dữ liệu hiệu quả trong tìm kiếm.
Đối với cây nhị phân tìm kiếm, dữ liệu giá trị của node con trái phải nhỏ hơn node cha. Giá trị của node con bên phải có giá trị lớn hơn lớp cha. Và giá trị nhỏ nhất chính là giá trị trái nhất, giá trị lớn nhất là giá trị phải nhất của cây
Biểu diễn cây tìm kiếm nhị phân trông giống như sau:

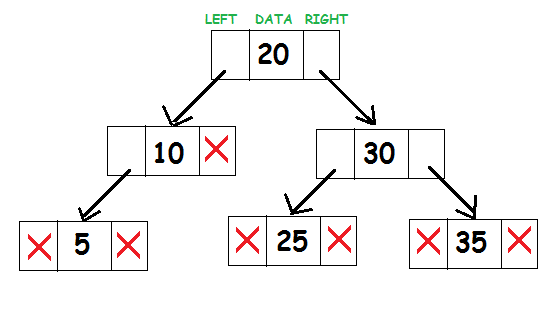
Xét nút gốc 20. Tất cả các phần tử ở bên trái của cây con (10, 5) nhỏ hơn 20 và tất cả các phần tử ở bên phải của cây con (25, 30, 35) đều lớn hơn 20.

Thực hiện BST

Đầu tiên, xác định một cấu trúc là tree_node. Nó sẽ lưu trữ dữ liệu và con trỏ tới cây con trái và phải.

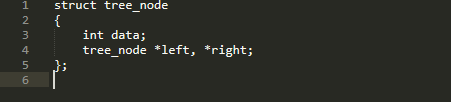
Bản thân nút rất giống với nút trong danh sách liên kết. Kiến thức cơ bản về mã cho danh sách liên kết sẽ rất hữu ích trong việc hiểu các kỹ thuật của cây nhị phân.

Hợp lý nhất là tạo một lớp cây tìm kiếm nhị phân để đóng gói các hoạt động của cây vào một khu vực duy nhất và cũng làm cho nó có thể tái sử dụng. Lớp sẽ chứa các hàm để chèn dữ liệu vào cây, tìm kiếm xem dữ liệu có tồn tại hay không và các phương thức để duyệt qua cây.

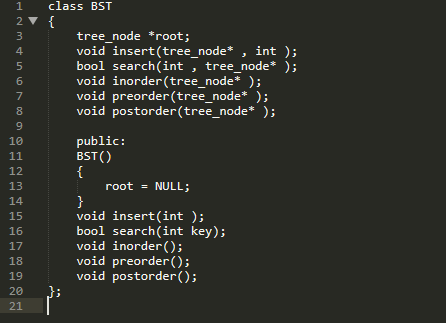
Cần khởi tạo root thành NULL để các hàm sau này có thể nhận biết nó không tồn tại.

Tất cả các thành viên công khai của lớp được thiết kế để cho phép người dùng của lớp sử dụng lớp mà không cần xử lý thiết kế bên dưới. Các hàm sẽ được gọi đệ quy là những hàm riêng tư, cho phép chúng di chuyển xuống dưới dạng cây.

Chèn dữ liệu vào trong một BST

Để chèn dữ liệu vào cây nhị phân bao gồm 2 bước. Một bước tìm kiếm một node ở vị trí thích hợp trong cây BST và bước hai là chèn giá trị khóa. Hàm chèn nói chung là một hàm đệ quy tiếp tục di chuyển xuống các cấp của cây nhị phân cho đến khi có một lá chưa sử dụng ở một vị trí tuân theo các quy tắc đặt các nút sau đây.

So sánh dữ liệu của nút gốc và phần tử sẽ được chèn.
Nếu dữ liệu của nút gốc lớn hơn và nếu tồn tại cây con bên trái, thì lặp lại bước 1 với root = gốc của cây con bên trái . Khác,
Chèn phần tử làm con bên trái của gốc hiện tại.
Nếu dữ liệu của nút gốc lớn hơn và nếu tồn tại cây con bên phải, thì hãy lặp lại bước 1 với root = gốc của cây con bên phải .
Ngược lại, chèn phần tử vào bên phải của phần tử gốc hiện tại.

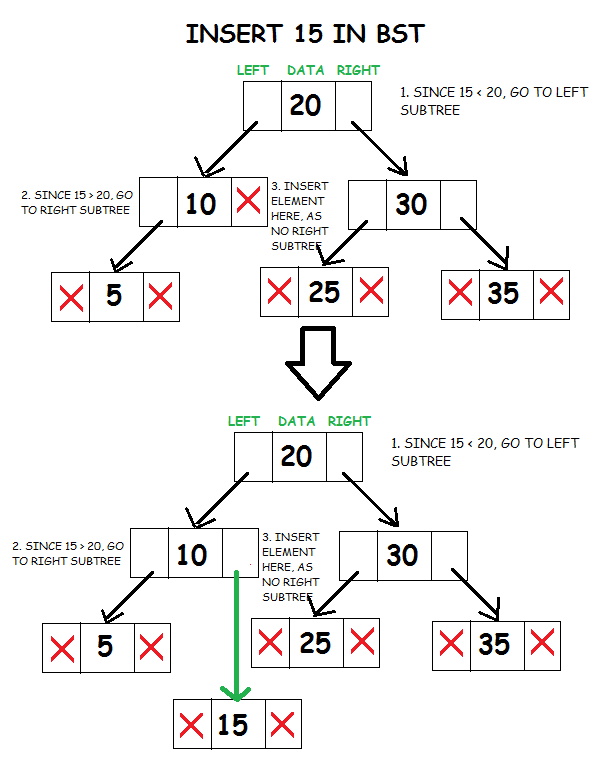
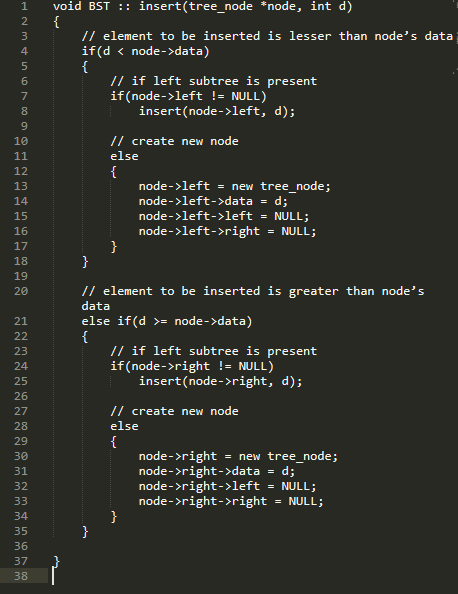
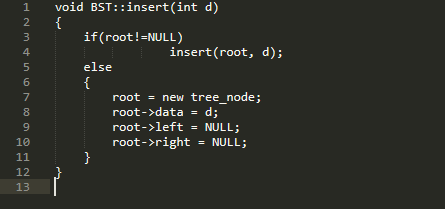
Vì nút gốc là một thành viên riêng tư, chúng tôi cũng viết một hàm thành viên công khai có sẵn cho những người không phải là thành viên của lớp. Nó gọi hàm đệ quy riêng để chèn một phần tử và cũng xử lý trường hợp khi nút gốc là NULL.

Tìm kiếm trong BST

Chức năng tìm kiếm hoạt động theo cách tương tự như chèn. Nó sẽ kiểm tra xem giá trị khóa của nút hiện tại có phải là giá trị cần tìm hay không. Nếu không, cần kiểm tra xem giá trị cần tìm có nhỏ hơn giá trị của nút hay không, trong trường hợp đó nó sẽ được gọi đệ quy trên nút con bên trái hoặc nếu nó lớn hơn giá trị của nút, nó phải được gọi đệ quy trên nút con bên phải.

So sánh dữ liệu của nút gốc và giá trị cần tìm.
Nếu dữ liệu của nút gốc lớn hơn và nếu tồn tại cây con bên trái, thì lặp lại bước 1 với root = gốc của cây con bên trái . Khác,
Nếu dữ liệu của nút gốc lớn hơn và nếu tồn tại cây con bên phải, thì hãy lặp lại bước 1 với root = gốc của cây con bên phải . Khác,
Nếu giá trị được tìm kiếm bằng với dữ liệu của nút gốc, trả về true.
Khác, trả về false.

Vì nút gốc là một thành viên riêng tư, chúng tôi cũng viết một hàm thành viên công khai có sẵn cho những người không phải là thành viên của lớp. Nó gọi hàm đệ quy riêng để tìm kiếm một phần tử và cũng xử lý trường hợp khi nút gốc là NULL.

Duyệt qua một BST

Chủ yếu có ba kiểu truyền cây:

Duyệt tiền thứ tự Pre-order (NLR):

Trong kỹ thuật này, chúng tôi làm như sau:

Xử lý dữ liệu của nút gốc.
Đầu tiên, đi qua cây con bên trái hoàn toàn.
Sau đó, đi qua cây con bên phải.

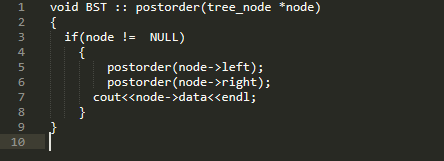
Duyệt hậu thứ tự – Post-order Traversal (NLR):

Trong kỹ thuật truyền tải này, chúng tôi thực hiện như sau:

Cây con đầu tiên đi ngang bên trái hoàn toàn.
Sau đó, đi qua cây con bên phải hoàn toàn.
Sau đó, xử lý dữ liệu của nút.

Duyệt trung thứ tự – In-order Traversal (LNR)

Để duyệt theo thứ tự, chúng tôi thực hiện như sau:

Cây con bên trái quy trình đầu tiên.
Sau đó, xử lý nút gốc hiện tại.
Sau đó, xử lý cây con bên phải.

Việc duyệt theo thứ tự của cây tìm kiếm nhị phân cung cấp thứ tự được sắp xếp của các phần tử dữ liệu có trong cây tìm kiếm nhị phân. Đây là một thuộc tính quan trọng của cây tìm kiếm nhị phân.

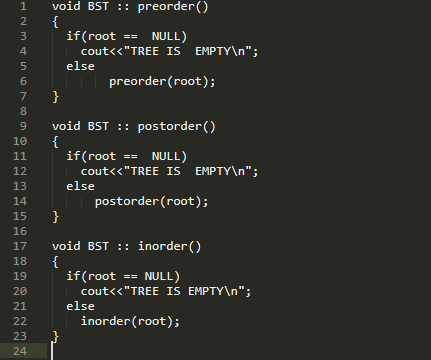
Vì nút gốc là một thành viên riêng, chúng tôi cũng viết các hàm thành viên công cộng có sẵn cho những người không phải là thành viên của lớp. Nó gọi hàm đệ quy riêng để duyệt qua cây và cũng xử lý trường hợp khi nút gốc là NULL.

Phân tích độ phức tạp

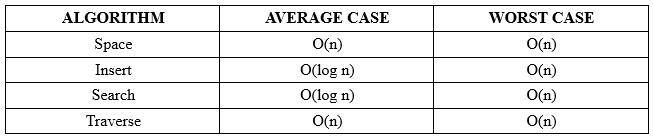
Độ phức tạp về thời gian của việc tìm kiếm và chèn phụ thuộc vào chiều cao của cây. Trung bình, cây tìm kiếm nhị phân có n nút có chiều cao là O (log n) . Tuy nhiên trong trường hợp xấu nhất, cây có thể có chiều cao là O (n) khi cây không cân bằng giống như một danh sách liên kết. Ví dụ trong trường hợp này:

Truyền tải yêu cầu O (n) thời gian, vì mọi nút đều phải được truy cập.

Ví dụ C++ về cây nhị phân tìm kiếm

Đây là một ví dụ của source code C++ cho Binary Search Tree (BST):

#include <iostream>

using namespace std;

struct Node
{
    int data;
    Node *left;
    Node *right;
};

Node *newNode(int data)
{
    Node *temp = new Node;
    temp->data = data;
    temp->left = temp->right = NULL;
    return temp;
}

Node *insert(Node *node, int data)
{
    if (node == NULL) return newNode(data);

    if (data < node->data)
        node->left = insert(node->left, data);
    else if (data > node->data)
        node->right = insert(node->right, data);

    return node;
}

bool search(Node *node, int data)
{
    if (node == NULL) return false;

    if (node->data == data)
        return true;
    else if (node->data < data)
        return search(node->right, data);
    else
        return search(node->left, data);
}

int main()
{
    Node *root = NULL;
    root = insert(root, 50);
    insert(root, 30);
    insert(root, 20);
    insert(root, 40);
    insert(root, 70);
    insert(root, 60);
    insert(root, 80);

    int searchValue = 60;
    if (search(root, searchValue))
        cout << searchValue << " found in the BST" << endl;
    else
        cout << searchValue << " not found in the BST" << endl;

    return 0;
}

Trong đó, hàm insert được sử dụng để chèn một giá trị vào cây. Nếu node đang xét là NULL, nó sẽ tạo mới một node với giá trị đã cho. Nếu giá trị muốn chèn nhỏ hơn giá trị của node, nó sẽ đi xuống cây trái. Ngược lại, nếu giá trị muốn chèn lớn hơn giá trị của node, nó sẽ đi xuống cây phải.

Hàm search được sử dụng để tìm kiếm một giá trị trong cây.

C/C++

Cây nhị phân và cây nhị phân tìm kiếm